代數K理論(的一個代數學分支。它的起源可追溯 到1958年格羅騰迪克(Grothendieck,A.)關於廣義 黎曼-羅赫定理的研究。這個學科的第一本專著是 1968年由巴斯(Bass,H.)完成的。
基本介紹
- 中文名:代數K理論
- 外文名:algebraic K-theory
- 時間:20 世紀60年代發展起來
- 研究範疇:阿貝爾群範疇的一系列函子
概念解釋
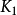
學科發展
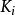

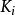
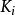
代數K理論(的一個代數學分支。它的起源可追溯 到1958年格羅騰迪克(Grothendieck,A.)關於廣義 黎曼-羅赫定理的研究。這個學科的第一本專著是 1968年由巴斯(Bass,H.)完成的。
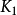
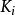

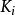
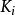
代數K理論(的一個代數學分支。它的起源可追溯 到1958年格羅騰迪克(Grothendieck,A.)關於廣義 黎曼-羅赫定理的研究。這個學科的第一本專著是 1968年由巴斯(Bass...
《代數K理論及其套用》是2010年1月1日世界圖書出版公司出版的圖書,作者是羅森博格。本書以1990年秋天Maryland大學講義為基礎,不僅為數學領域研究生提供很好的學習代數...
最早由亞歷山大·格羅滕迪克1957年發現,名字取自德文“Klasse”,意為“分類”class 。在數學中,K-理論(K-theory)是多個領域使用的一個工具。在代數拓撲中,它是...
K理論(荷)(K一Theory ) ( Dordrecht ) 1987年創刊.刊號:510I_B057 } ISSN0920-3036.荷蘭Kluwer學術出版集團出版。...
在數學中,代數L理論(L-theory)是K理論的二次型,而“L”的命名緣由即意味著它來自於“K理論”(L是K後面的一個字母)。L理論一個較為人所知的稱呼是“厄米K...
《代數數理論講義》是2005年科學出版社出版的圖書,作者是赫克。...... 本書向讀者介紹了構成代數數論理論框架的一般...§30. 有理素數的第二型分解定理:域K(e2...
一個代數數是某一方程式的根。代數數的理論——伽羅瓦理論是數學中最令人滿意的...——記為乘法的從K×E到E中的映射(α,x)↦αx,這是一個作用法則;...
高階K群(higher K-group)格羅滕迪克群(K。群)、懷特海群(K:群)、施坦貝格群的中心(Kz群)的推廣及一般化.代數K理論的重要研究對象.n妻3時,K。群稱為高...
《數學概覽:代數基本概念》文前附季理真撰寫的有關作者及《代數基本概念》內容的...B.代數K-理論 投射模類的群.環的Ko,K1和Kn域的K2及其與Brauer 群的關係...
域論是代數數論的重要理論之一。它深刻地刻畫了(相對)阿貝爾擴張。代數元(algebraic element)是域論的基本概念之一。設K是域F的擴域,K中元α稱為F上代數元,是...
霍普夫代數是20世紀60年代以後迅速發展起來的代數學的新學科。域k上的霍普夫代數是同時具有k代數結構和它的對偶結構(k余代數結構)並滿足一定的相容條件的代數系統。...
一個代數數是某一方程式的根。代數數的理論——伽羅瓦理論是數學中最令人滿意的...設K為一交換體. 把K上的向量空間E叫做K上的代數,或叫K-代數,如果賦以從E...
概形理論里的許多概念都能推廣到代數空間,並且代數空間中包含有扎里斯基拓撲意義...若V是域k上的代數簇,則RatR(V)稱為V的函式域。設f是X到Y的有理映射,...
a:點集拓撲學 b:代數拓撲學 c:同倫論 d:低維拓撲學 e:同調論 f:維數論 g:格上拓撲學 h:纖維叢論 i:幾何拓撲學 j:奇點理論 k:微分拓撲學 l:拓撲學...
