人口系統數學模型,用來描述人口系統中人的出生、死亡和遷移隨時間變化的情況,以及它們之間定量關係的數學方程式或方程組,又稱人口模型。
正文
20世紀30年代A.J.洛特卡建立了人口的定常積分方程模型。40年代萊斯利建立了差分方程組模型。60年代又出現了弗爾斯特的偏微分方程模型。70年代波拉德在萊斯利模型基礎上提出了隨機模型。建立完善的人口系統閉環控制模型,則是最近幾年的事。中國控制論學者在這項工作中取得了重要成果。
模型
人口系統連續模型 兩個自變數的函式()代表時刻一切年齡小於的人口總數,稱為人口函式。(=媆()/媆,稱為人口密度函式。則人口系統連續模型為
實際上,嗘()應與時刻的人口狀態,特別是與處在生育期內婦女的生育水平有密切關係。考慮到這一特點又有如下的人口閉環控制模型:
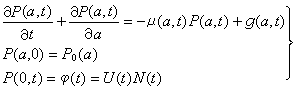 人口系統數學模型
人口系統數學模型在模型(2)中,嗘()與時刻的人口狀態()建立了直接關係,這在控制論中稱為實時狀態反饋,這種控制形式稱為閉環控制(見閉環控制系統)。
人口系統離散模型 如果用(),(),(),…,()表示時刻的年齡構成,其中()表示年代年滿周歲但不到+1周歲的人口數,寫成向量形式
則離散人口模型可寫成
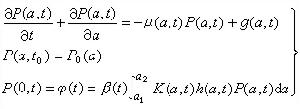 人口系統數學模型
人口系統數學模型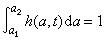 人口系統數學模型
人口系統數學模型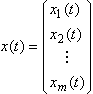 人口系統數學模型
人口系統數學模型式中稱為按齡死亡率,為人類能活到的最高年齡;稱為嬰兒死亡率;()為女性比例函式;()為婦女生育模式,服從歸一化條件;()為人口遷移向量;為人口初始年齡狀態;()為婦女總和生育率,它是系統控制變數;()是人口狀態變數。模型(3)是一個雙線性系統。在這個模型中,一項是年代人口經死亡後留存到下一年的人口年齡構成。而是年代出生的人口留存到下一年的人口,()是年代遷移人口留存到下一年的人口。在模型(3)中,方程左端表示+1年代的人口年齡構成,而方程右端則表現了年代人口年齡的變化。因此在這個模型中,時間、出生、死亡和遷移四個因素以及它們之間的定量關係得到了完全描述。
在模型(1)、(2)、(3)中,觀測變數就是人口指數,例如總人口數()
人口控制就是通過改變、調節婦女總和生育率()來控制人口狀態(),達到改變和控制人口趨勢的目的。
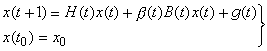 人口系統數學模型
人口系統數學模型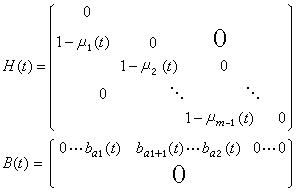 人口系統數學模型
人口系統數學模型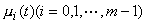 人口系統數學模型
人口系統數學模型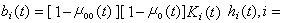 人口系統數學模型
人口系統數學模型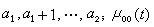 人口系統數學模型
人口系統數學模型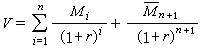 人口系統數學模型
人口系統數學模型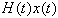 人口系統數學模型
人口系統數學模型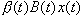 人口系統數學模型
人口系統數學模型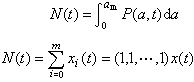 人口系統數學模型
人口系統數學模型