亞橢圓運算元是一類重要的擬微分運算元,是橢圓型擬微分運算元的推廣。
基本介紹
- 中文名:亞橢圓運算元
- 外文名:hypoelliptic operator
- 領域:數學
- 屬性:擬微分運算元
- 作用:橢圓型擬微分運算元的推廣
- 相關名詞:橢圓運算元
簡介,主型運算元的亞橢圓性條件,橢圓型擬微分運算元,
簡介
亞橢圓運算元是一類重要的擬微分運算元,是橢圓型擬微分運算元的推廣。設
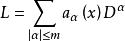
其中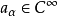 ,微分運算元L稱為亞橢圓的若且唯若對任意
,微分運算元L稱為亞橢圓的若且唯若對任意 。換言之,L 是亞橢圓的若且唯若對任一開集
。換言之,L 是亞橢圓的若且唯若對任一開集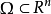 和
和 ,如果
,如果 ,則有
,則有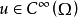 ,具有
,具有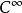 係數的橢圓型偏微分運算元和具有
係數的橢圓型偏微分運算元和具有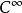 係數的拋物型偏微分運算元都是亞橢圓運算元。如果P是擬微分運算元,並且對任何
係數的拋物型偏微分運算元都是亞橢圓運算元。如果P是擬微分運算元,並且對任何 ,有
,有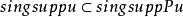 ,也稱P是亞橢圓運算元。由於橢圓型擬微分運算元的內正則性(參見“橢圓型方程解的正則性”),因此橢圓型擬微分運算元也是亞橢圓運算元。
,也稱P是亞橢圓運算元。由於橢圓型擬微分運算元的內正則性(參見“橢圓型方程解的正則性”),因此橢圓型擬微分運算元也是亞橢圓運算元。
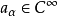

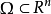


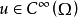
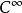
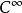

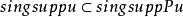
主型運算元的亞橢圓性條件
對於使主象徵,
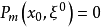
的每點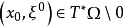 及使
及使
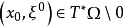
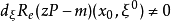
的每個複數z,有: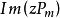 沿
沿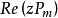 的過
的過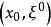 的零次特徵帶不變號,並且在
的零次特徵帶不變號,並且在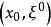 的任何鄰域內沿該零次特徵不恆為0。對於一般情形下的亞橢圓性判別問題還尚未解決。
的任何鄰域內沿該零次特徵不恆為0。對於一般情形下的亞橢圓性判別問題還尚未解決。
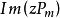
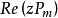
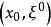
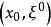
橢圓型擬微分運算元
在偏微分方程理論中,在開放子集上定義了偏微分運算元P:(Hypoelliptic operator)
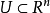
對於在開放子集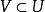 上定義的每個分布u,如果Pu是
上定義的每個分布u,如果Pu是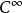 ,u也必須是
,u也必須是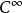 。
。
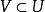
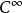
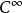
如果這個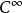 替換為實際解析,則P被稱為解析亞橢圓。
替換為實際解析,則P被稱為解析亞橢圓。
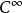
具有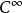 係數的每個橢圓運算符都是亞橢圓。
係數的每個橢圓運算符都是亞橢圓。
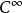
特別地,拉普拉斯運算元是一個亞橢圓運算符的例子(拉普拉斯運算元也是分析上的低橢圓)。熱方程運算符
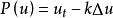
是亞橢圓的(其中k> 0),但不是橢圓的。 波動方程運算符
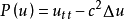
不是亞橢圓的(其中c≠0)。