互為餘角

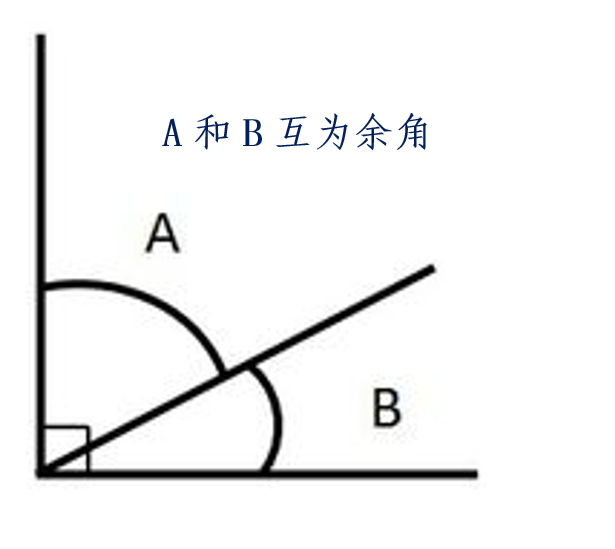
互為餘角是描述兩個角之間數量關係的數學名詞。若兩角之和為90°，則稱這兩個角“互為餘角”，簡稱“互余”。若兩個角互為餘角，則可以說其中一個角是另一個角的餘角。

基本介紹

• 中文名：互為餘角
• 外文名：complementary angle
• 簡稱：互余
• 描述：兩個角之間數量關係
• 基本釋義：兩角之和為90°，則兩角互為餘角
• 學科：數學
• 領域：幾何、三角函式

定義

如果兩角之和為90°，那么我們就說這兩個角互為餘角，簡稱互余，也可以說其中一個角是另一個角的餘角。例如：

∠A=30°，∠B=60°，∴∠A+∠B=90°，則稱“∠A與∠B互為餘角”。

∠A=15°，∠B=75°，∴∠A+∠B=90°，則稱“∠A與∠B互為餘角”。

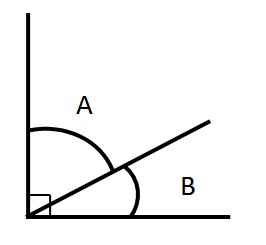∠A與∠B互為餘角

性質

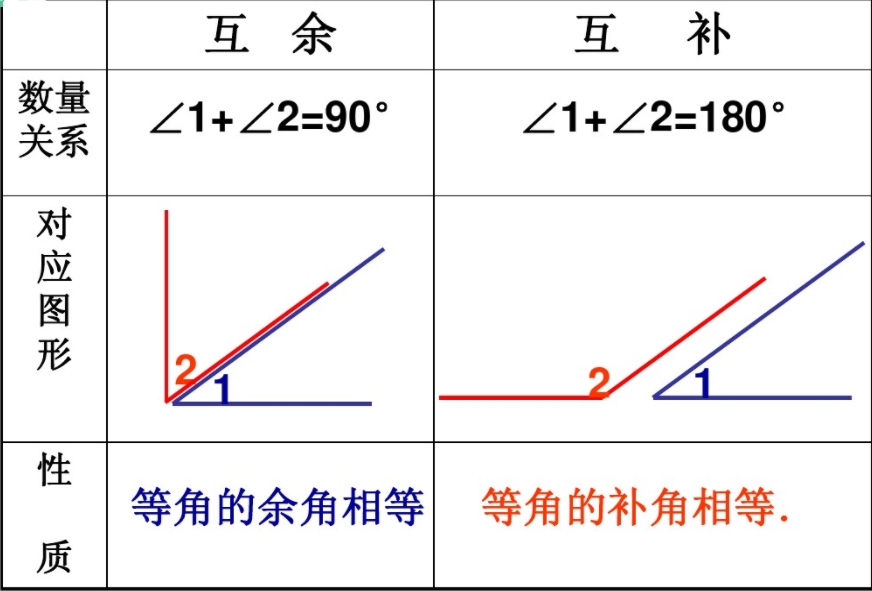
（1）同角的餘角相等

比如：∠A+∠B=90°，∠A+∠C=90°，則：∠C=∠B。

（2）等角的餘角相等

比如：∠A+∠B=90°，∠D+∠C=90°，∠A=∠D，則：∠C=∠B。

注意

（1）“互為餘角”是兩角之間的數量關係，與兩個角的位置無關

（2）“互余”概念中的角總是成對出現

（3）只有銳角才有餘角

互余和互補

互補（互為補角）也是描述兩個角之間關係的數學名詞。若兩角之和為180°，則稱這兩個角“互為補角”，簡稱“互補”。若兩個角互為互補，則可以說其中一個角是另一個角的補角。

互余和互補之間的對比如下圖。

三角函式方面

若A和B互為餘角，即A+B=90°，則有

（1） sinA=cosB，cosA=sinB

（2） tanAtanB=1 （tanA，tanB均不等於0）

（3） tanA = cotB

例題

∠1和∠2互為餘角，∠1=(6x+8)°，∠2=(4x-8)°，求∠1和∠2的度數。

解：

∵ ∠1和∠2互為餘角

∴∠1+∠2=90°

又∵∠1=(6x+8)°，∠2=(4x-8)°

∴ 6x+8+4x-8=90

∴ x=9

∴∠1=62°， ∠2=28°