中值濾波法是一種非線性平滑技術，它將每一像素點的灰度值設定為該點某鄰域視窗內的所有像素點灰度值的中值.
中值濾波是基於排序統計理論的一種能有效抑制噪聲的非線性信號處理技術，中值濾波的基本原理是把數字圖像或數字序列中一點的值用該點的一個鄰域中各點值的中值代替，讓周圍的像素值接近的真實值，從而消除孤立的噪聲點。方法是用某種結構的二維滑動模板，將板內像素按照像素值的大小進行排序，生成單調上升（或下降）的為二維數據序列。二維中值濾波輸出為g（x,y）=med{f(x-k,y-l),(k,l∈W)} ，其中，f(x,y)，g(x,y)分別為原始圖像和處理後圖像。W為二維模板，通常為3*3，5*5區域，也可以是不同的的形狀，如線狀，圓形，十字形，圓環形等。
基本介紹
- 中文名：中值濾波
- 外文名：median filtering
- 套用學科：通信；圖像處理
定義,實現方法,套用,
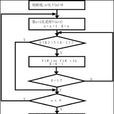
定義
中值濾波對脈衝噪聲有良好的濾除作用，特別是在濾除噪聲的同時，能夠保護信號的邊緣，使之不被模糊。這些優良特性是線性濾波方法所不具有的。此外，中值濾波的算法比較簡單，也易於用硬體實現。所以，中值濾波方法一經提出後，便在數位訊號處理領得到重要的套用。
中值濾波方法：對一個數位訊號序列xj(-∞<j<∞)進行濾波處理時，首先要定義一個長度為奇數的L長視窗，L=2N+1，N為正整數。設在某一個時刻，視窗內的信號樣本為x(i-N)，…，x(i)，…，x(i+N)，其中x(i)為位於視窗中心的信號樣本值。對這L個信號樣本值按從小到大的順序排列後，其中值，在i處的樣值，便定義為中值濾波的輸出值，寫為如圖1.
圖1
圖1中值濾波是在“最小絕對誤差”準則下的最優濾波。
在實際套用中，隨著所選用視窗長度的增加，濾波的計算量將會迅速增加。因此，尋求中值濾波的快速算法，是中值濾波理論的一個重要研究內容。中值濾波的快速算法，一般採用下述三種方式：①直方圖數據修正法；②樣本值二進制表示邏輯判斷法；③數字和模擬的選擇網路法。
對中值濾波的理論研究，還集中於統計特性分析和根序列的描述方面。當一個信號序列經一特定視窗長度的中值濾波反覆處理後，它會收斂於某一個不再變化的序列，這個序列稱為中值濾波的根序列。根序列是描述中值濾波特性的一個重要概念。通過對根序列結構的研究，可以確定原信號序列中，哪些成分可以經中值濾波後保留下來，哪些成分將被抑制。這對確定中值濾波器的視窗長度，提供了重要依據。用VLSI實現的中值濾波器晶片，可供實時處理中套用。
實現方法
1：通過從圖像中的某個採樣視窗取出奇數個數據進行排序
2：用排序後的中值取代要處理的數據即可
