中介邏輯(medium logic)在中介原則觀點下建立起來的一種非經典邏輯.狹義地,中介邏輯僅指中介邏輯演算系統ML.廣義地,中介邏輯除了它的基礎部分,即演算系統ML之外,還應包括中介公理集合論系統MS,以及後來發展起來的中介代數系統、中介模態邏輯、中介邏輯的根岑系統、中介模型論等.廣義中介邏輯簡記為MM
基本介紹
- 中文名:中介邏輯
- 外文名:mediation logic
- 關鍵字:非經典邏輯 模糊數學
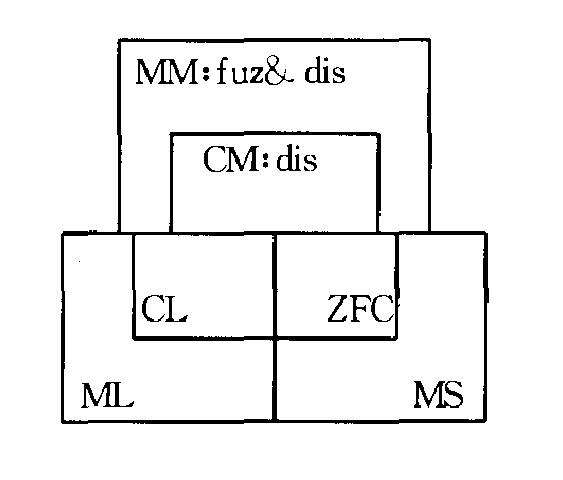
中介邏輯(medium logic)在中介原則觀點下建立起來的一種非經典邏輯.狹義地,中介邏輯僅指中介邏輯演算系統ML.廣義地,中介邏輯除了它的基礎部分,即演算系統ML之外,還應包括中介公理集合論系統MS,以及後來發展起來的中介代數系統、中介模態邏輯、中介邏輯的根岑系統、中介模型論等.廣義中介邏輯簡記為MM

中介邏輯(medium logic)在中介原則觀點下建立起來的一種非經典邏輯.狹義地,中介邏輯僅指中介邏輯演算系統ML.廣義地,中介邏輯除了它的基礎部分,即演算系統ML之外,還應包括中介公理集合論系統MS,以及後來發展起...
邏輯中介是運用從抽象上升到具體的方法以形成系統理論而確定的、聯結起點和終點之間的、由一系列概念、範疇所組成的中間環節。亦即邏輯範疇體系中的邏輯中項,即中介範疇。邏輯終點運用從抽象上升到具體的方法以形成系統理論最後所獲得的最...
中介公理集合論(medium axiomatic set theory)一種公理集合論系統.是以中介邏輯演算MI,為邏輯推理工具的非經典的公理集合論系統(記為MS).詳細介紹 它由21條非邏輯公理(模式)構成,其中以泛概括公理為核心.在MS中,首先給出了有如 等...
Klein(1973) 認為多樣化成本是出現金融中介的必要條件,並且注意到這“提供了一種聚合資財的經濟刺激,而中介機構則是如此聚合資財的合乎邏輯的工具”。 Kane & Buser(1979) 研究了美國商業銀行持有證券的多樣化程度。金融中介的規模經濟...
黑格爾認為,作為事物之間聯繫環節和事物轉化、發展中間環節的中介,是普遍存在的。黑格爾把與直接性相對的中介概念運用於認識論,批評了那種認為普遍真理是直接地呈現在人的意識面前,僅僅屬於理智直觀或信仰的對象,而無需以經驗和邏輯思維...
《數學無窮與中介的邏輯基礎》是2012年科學出版社出版的圖書,作者是朱梧檟。內容簡介 《數學無窮與中介的邏輯基礎》是一部研究型的原創著作,全書分6章和1個附錄。第1、2兩章討論經典與非經典數學的基礎問題,其核心主題是介紹中介數學...
①邏輯語義原則:同傳統語法中劃分句子成分的原則基本一致。根據這一原則,劃分出6大類句子成分,即主語類 、謂語類、賓語類 、補語類、定語類、狀語類。插入成分和獨立成分是狀語的兩個次類。層次原則 ②結構層次原則:句子是分層次的...
第二節 人——令客觀事物為己所用的中介 第三節 人類已構建的四大虛擬世界 下篇 人類文明的雲梯——邏輯:方法論 第八章 經典邏輯的困惑 第一節 什麼是邏輯 第二節 空間邏輯的困惑 第三節 時間邏輯的困惑 第四節 科學相對論的...
金融中介機構理論是關於非銀行金融中介機構在創造信用、影響投資、儲蓄和產出等方面具有與銀行體系同樣地位和作用的學說。是對美國經濟學家麥金農的金融抑制論和美國著名學者E. S·肖的金融深化論,以及其他經濟學者在此基礎上進行進一步發展...
邏輯中介 馬克思認為,理解資本主義生產方式的困難在於:貨幣轉化為資本必須根據商品交換的內在規律來說明,而貨幣轉化為資本的流通形式又是與商品、價值、貨幣的性質,與商品交換的規律相矛盾的。因此,作為科學認識的關節點就在於,要從邏輯...
理性具象思維:感性具體基礎上經過思維的分析和綜合,達到對事物多方面屬性或本質的把握。由抽象上升到具體的方法,就是由抽象的邏輯起點經過一系列中介,達到思維具體的過程。目的性 上升性思維:以實踐所提供的個別性經驗為起點,把個別...
“邏輯思維”具有多樣性,包括:正向思維、逆向思維、橫向思維、發散思維。增強各自含義的理解,有助於您及早形成正確的思維方向。正向思維 思維本沒有正向和逆向之分,我為了了解區分思維,給思維分類下了這樣的一個概念。“我把常規的...
辯證邏輯是研究人的認識理性階段思維規律的學說,含矛盾邏輯與對稱邏輯兩大類型或兩個階段。辯證邏輯(dialectical logic)作為邏輯學的辯證法,研究反映客觀世界的辯證發展過程的人類思維的形態,即關於辯證思維的形式、規律和方法的科學。辯...
1 989年調南京航空航天大學計算機系任教,主要從事數學基礎、數理邏輯和計算機科學理論等方向的研究。迄今個人或與他人合作發表論文190餘篇.出版著作7部.譯著l部。l983年以來,與肖奚安教授長期合作研究,創建和發展了中介邏輯演算和中介...
可知,MS系統中的泛概括公理又在實際上全面保留了康托爾意義下概括原則的內容.這樣,“在MS系統中是否會出現悖論”的問題就可做出肯定的回答:不會.在MS系統中已嚴格證明,歷史上任何邏輯數學悖論,以及在二值系統內無需解釋的多值邏輯...
根據思維的形態,可以把思維分成動作思維、形象思維和抽象思維。其中抽象思維是用詞進行判斷、推理並得出結論的過程,又叫詞的思維或者邏輯思維。抽象思維以詞為中介來反映現實,這是思維的最本質特徵,也是人的思維和動物心理的根本區別。...
謂詞演算系統在數理邏輯中,命題邏輯的系統是謂詞邏輯系統的子系統,故命題演算系統的所有東西都可以當做謂詞邏輯的推演依據。在數理邏輯中,命題邏輯的系統是謂詞邏輯系統的子系統,故命題演算系統的所有東西都可以當做謂詞邏輯的推演依據。命...
由抽象上升到具體的方法,就是由抽象的邏輯起點經過一系列中介,達到思維具體的過程。邏輯歷史 由抽象上升到具體的邏輯思維過程同客觀事物的歷史過程和認識的歷史過程應當符合,也就是邏輯和歷史的統一。邏輯指的是理性思維或抽象思維,它以...
