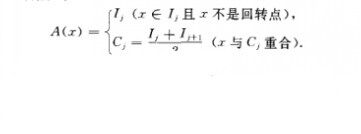

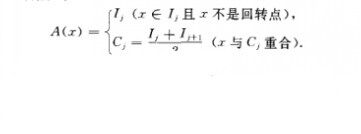

不變坐標(invariant coordinate)一類由點的疊代運動決定的形式序列或形式冪級數.對於逐段單調映射.f :l-"1,以li,lz,...,1,記f的按自然順序排列的全部區段,C,GCZG...GC,_,為f的全部迴轉點.令 構造點xEl疊代運動的旅行圖A...
兩個及以上的坐標轉換時由極坐標相對參照確定維數空間。含義 坐標變換共有五種,除平移外均以坐標原點為基準點,即變換前後坐標原點不變。下面給出五種基本變換的中英文名稱和矩陣描述。基本變換 多維視圖 二維 三維 變倍 scale 二維 ...
變值坐標系是一種坐標系。在現代數學中,比較常用的常規坐標系可有五種,而上述箱變坐標系只是對常規直角坐標系的初步擴展,此時可叫等基方法(包括等基等值和等基變值。正箱體簡介 的最初嘗試來自求解正箱體頂底面的扭面方程,故...
中心不變定理說的是任何宇宙系統在不受外來聯結能破壞的情況下,將保持系統中心坐標不變。這裡所說的坐標是統一論的連續統空間中的坐標。這條定理表明在討論一個具體的宇宙系統時,其中心是最好的參照點。系統中心概念是經典理論中質心...
廣義不變性 廣義不變性為物理定律的形式在任意微分坐標轉換下保持不變。其精神在於坐標並非先驗地存在於自然中,而是人們欲描述自然所伴隨的人工產物;也因此不應在基本物理定律中具有實質物理意義。
變化時,則 表示共焦橢球坐標系。因為u在該區間內有 故方程 具有橢球面方程的形式, 和 表示變化的半主軸長度,半主軸的變化就形成一系列共焦橢球曲面,如圖1所示。(3)當 在區間 變化時,則 表示共焦單葉雙曲面坐標系...
乘積不變性(product invariance)在乘積運算下保持不變的拓撲性質.設屍表示某個拓撲性質,若當每個坐標空間Xa(aED)具有性質P時,積空間 也具有性質P,則稱性質屍為乘積不變性或可積性.例如,豪斯多夫分離性是乘積不變性,連通性和緊性...
坐標系變化 1:柱坐標系(r,φ,z)與直角坐標系(x,y,z)的轉換關係:x=rcosφ y=rsinφ z=z 2:同樣的,直角坐標系(x,y,z)與柱坐標系(r,φ,z)的轉換關係:r= φ=arctan(y/x)z=z ...
f(x,y)和g(x,y)的極坐標形式分別為f(ρ,θ)和g(p,θ),上面的公式可寫成下面的形式:g(p,θ)=f(ρ/θ,θ-θ0)f(ρ,θ)和g(p,θ)分別沿方向ρ取對數,得到 f(λ,θ)=f(logρ,θ)g(λ,θ)=g(logρ,θ)...
在局部坐標卡下,前一定義是後一定義的特款。雙曲不動點在C小擾動下不會消失的動力行為在結構穩定性研究中有著重要的作用,例如,在雙曲不變集及安諾索夫系統的結構穩定性的證明中就是如此。緊流形上的不動點都是雙曲的微分同胚集合...
本書為量子力學、量子光學和固體物理提供了新方法,也為經典力學的簡正坐標理論提供了新思路。適用群體 《量子力學的不變本徵算符方法》適合對量子論有興趣的廣大學生、教師和理論科研人員閱讀。圖書目錄 第1章 不變本徵算符(IEO)方法...
《直角坐標系的變化對平面內同一個點的坐標影響》是冶源鎮楊善國中提供的微課課程,主講教師是肖學紅。知識點 1.青島版/七年級下冊/第14章 位置與坐標 2.青島版/七年級下冊/第14章 位置與坐標/14.3 直角坐標系中的圖形。設計思路...
同樣地,其它兩個基坐標也會變化為其它的方向。進一步我們指出,如果說空間中的向量(因為任何一個向量都可以用無關的基向量表述)。我們可以想像,在這種變換矩陣的作用下,能否找到空間中某一個向量經過這種方式變換以後,具有和原來的...
洛倫茲變換是狹義相對論中兩個作相對勻速運動的慣性參考系(S和S′)之間的坐標變換。若S系的坐標軸為X、Y和Z,S′系的坐標軸為X′、Y′和Z′。為了簡單,讓X、Y和Z軸分別平行於X′、Y′和Z′軸,S′系相對於S系以不變速度...
通過這種方法,使用與前面一樣的矩陣乘積可以將各種變換無縫地集成到一起。當使用仿射變換時,其次坐標向量w從來不變,這樣可以把它當作為 1。但是,透視投影中並不是這樣。透視投影:三維計算機圖形學中另外一種重要的變換是透視投影。與...
這個理論的出發點是兩條基本假設:狹義相對性原理和光速不變原理。理論的核心方程式是洛倫茲變換(群)(見慣性系坐標變換)。狹義相對論預言了牛頓經典物理學所沒有的一些新效應(相對論效應),如時間膨脹 、長度收縮、橫向都卜勒效應、...
正則變換是由一組正則變數到另一組能保持正則形式不變的變數的變換。在哈密頓力學裡,正則變換(canonical transformation)是一種正則坐標的改變,(q,p)-->(Q,P),而同時維持哈密頓方程的形式,雖然哈密頓量可能會改變。正則變換是...
第一類正交變換不改變直角坐標系的定向,即左(右)手系變換後仍是左(右)手系。注意:丨A丨=±1是變換σ成為正交變換的必要不充分條件。性質 (1)正交變換 不會改變向量間的正交性,如果 和 正交,則 和 亦為正交。(2)如果...
其中(x)是平面上點的射影坐標,(u′)是與(x)對應的直線的線坐標。射影變換 在歐氏平面上,對於“一組有定方位的一切直線”添加一個點稱為該方位的無窮遠點,此點在該組中的每一直線上,而不在這組以外的直線上;為了區分,...
因此,以坐標原點作為中心的中心仿射變換的公式是行列式不等於零的齊次線性變換。反之,行列式不等於零的齊次線性變換總表示中心仿射變換(我們還知道它同時可以表示坐標原點不變的仿射坐標變換)。
微分同胚共變性 微分同胚共變性為物理定律的形式在任意微分坐標轉換下保持不變。其精神在於坐標並非先驗地存在於自然中,而是人們欲描述自然所伴隨的人工產物;也因此不應在基本物理定律中具有實質物理意義。
