變值坐標系

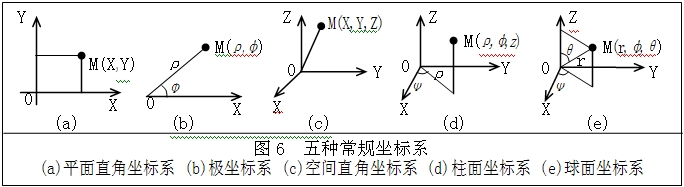
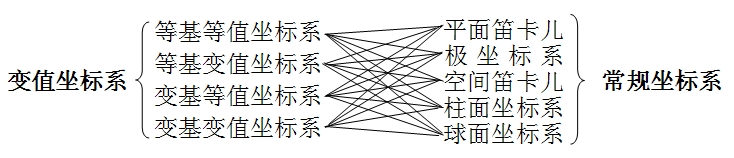
變值坐標系是一種坐標系。在現代數學中，比較常用的常規坐標系可有五種（圖6），而上述箱變坐標系只是對常規直角坐標系的初步擴展，此時可叫等基方法(包括等基等值和等基變值。

基本介紹

• 中文名：變值坐標系
• 套用於：現代數學
• 比較常用：五種
• 等基方法：等基等值和等基變值

正箱體簡介

的最初嘗試來自求解正箱體頂底面的扭面方程，故簡介如下：

1.1、正箱體的數學約定

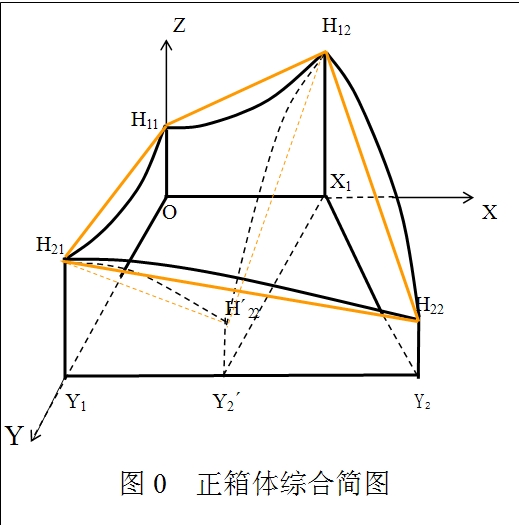
正箱體的概念來自常規箱體(如長方體)，但又與之有所不同。所謂正箱體是指有四個側面同垂(或正交)於某一平面的凸棱六面體(或叫六面凸稜體，如圖1)。這裡的凸稜體是指各相鄰側面所構成的內角均不大於π值的空間體，以避免對應坐標網線的相互交叉。正箱體是常規儲量計算塊段(如各種投影法的儲量計算塊段)的一種常見形態，因其尚無適當的通用術語而又具有常規箱體“四壁同垂(正交)一面”的基本特徵而故名(正箱體也可簡稱為箱體或箱)。正箱體可視為是對常規箱體的擴展，比常規箱體更具普遍性。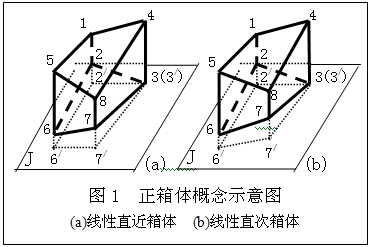

其中，正箱體的四個側面分別稱為橫側面(如圖中1234、5678)和縱側面(如圖中5621、8734)，剩餘兩面稱為頂底面(如圖中5841、6732)。其中，四個側面既可為平面，也可為直線型曲面(如柱狀拋物面)；頂底面可為平面、曲面或各種扭面。正箱體的縱、橫側面之交線叫高棱(圖中12、34、56、78)，頂底面間與高棱同向的直線叫高線，側面上的高線叫側線，所有側線和高線均為直線且相互平行。與四個側面同垂的平面叫基平面(圖中的J面)，四個側面在基平面上的投影叫基底或箱基或箱底(圖中6/7/3/2/)，在不致引起誤解時，基平面和基底均可稱為基面。兩個橫側面間的縱向距離叫長距，兩個縱側面間的橫向距離叫寬距，頂底面間的高線長度叫高距。由於長距、寬距和高距均為處處可變，故又可統稱為變距。這裡的長距、寬距和高距與相互垂直的三度方向相對應，其中的長距和寬距概念不同於通常的長度和寬度。正箱體任意內插位置的高距可由其四個側面的對應高距所決定，亦即內插高距的變化特徵對應於頂底面的線性或非線性扭面。所謂扭面可由一條母線沿著兩條異面導線適當移動或伴有某種變化而成，因其兩條異面導線常可由某種常規的同面導線經適當扭動而成而故名，其扭動角度可叫扭面角或扭角。當導線和母線均為直線時則為線性扭面(圖1)，否則，既可為非線性扭面也可為線性扭面(圖2)。而常規的平面和曲面只不過是扭面角為0的一種特例，因此，扭面是客觀存在的更為廣泛的基本面型。扭面可有單形與復形之分，所謂單形扭面是指該扭面可由一個連續型扭面方程來表達，否則為復形扭面，此處只討論單形扭面。

1.2、正箱體的數學分類

如圖2所示(圖中為標準正箱體，也可為一般正箱體)，按各側面的相互關係可將正箱體分為近箱體和次箱體兩個大類，其中，近箱體是指有兩個側面相互平行的正箱體[比較接近常規箱體，圖中(a)～(d)]，次箱體是指任意兩個不相鄰側面均不平行的正箱體[與常規箱體的差別較大，圖中(e)～(h)]。近箱體又可分為等長近箱體(兩個橫側面平行)和等寬近箱體(兩個縱側面平行)。將近箱體和次箱體進行比較可知，前者又可視為後者的特殊情形，亦即後者可以包含前者。當正箱體有三個共點側面為互垂平面時可叫標準正箱體，否則叫一般正箱體。一般正箱體均可通過降維變換(變換方法見後)而成標準正箱體。按基面或側面形狀，兩種正箱體(近箱體和次箱體)均可分為：直箱體(基面為直邊四邊形)和曲箱體(基面為曲邊四邊形，曲邊既可內凸也可外凸)。其中，直箱體中的近箱體還可分為方箱體(基底面為矩形)和梯箱體(基底面為梯形)；而曲箱體又可分為單曲箱體(只有長距或寬距為曲線變化)和雙曲箱體(長距和寬距均為曲線變化)，標準曲近箱體均為單曲箱體或可變為單曲箱體，曲次箱體既可為單曲箱體也可為雙曲箱體。按頂底面的變化特徵(由正箱體的高距變化特徵所決定)可分為線性正箱體(兩底為平面或線性扭面)與非線性正箱體(兩底為曲面或非線性扭面，既可上凸也可下凸)。其中，線性直箱體頂底面的對應導線和母線均為空間直線，而線性曲箱體的頂底面雖為線性扭面，但其對應導線和母線均可為空間曲線。將上述分類進行組合可得四種基本類型，即：線性直箱體、線性曲箱體、非線性直箱體、非線性曲箱體。故正箱體共有上述8種基本類型。由上述可知，常規的箱體(長方體)為正箱體的最簡單類型。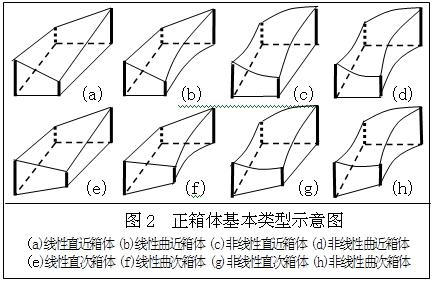

箱變坐標系簡介

由於箱變坐標系的最初靈感來自扭面方程的最初嘗試，故這裡首先對其作一簡要說明。

2.1、扭面方程的最初思路

在上述正箱體中，扭面可有線性與非線性之分，其對應方程(即扭面方程)亦有線性與非線性兩種基本類型。

(1)線性扭面方程：如圖3所示，圖中實線為一線性直近箱體，M1、M2兩面相互平行但不等寬，頂面為一簡單線性扭面。試求其對應方程。下面分兩種情形求之：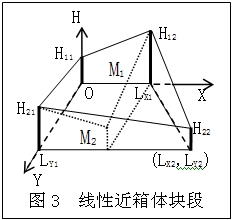

情形一：當M1、M2兩面平行等寬(圖中虛線)時則與方箱體相對應，該線性扭面上各點的對應高距沿縱、橫方向(嚴格說是坐標線方向)均呈線性變化。因此，可有常規方法直接推導法求得各點對應高距的線性扭面方程。

情形二：當M1、M2兩面平行但不等寬（圖3中的實線）或等寬但不平行或既不平行也不等寬時，則該扭面方程將難以採用常規方法直接求出。但若適當改變M1、M2兩面間的空間密度，使之變為等長等寬的不等密空間，或適當改變坐標單位使兩面間的縱、橫坐標單位數各自處處對應相等，便可仿照情形一那樣運用常規方法(採用對應坐標單位數)直接求出其扭面方程。其基本方法是：先設定某一基準坐標單位(如坐標軸上的坐標單位)，然後將其乘以某一非0係數(叫坐標係數，可為某一函式)。以上便是解決各種扭面問題的最初思路和方法。

(2)非線性扭面方程：如圖4所示，圖中實線為一非線性近箱體(也可為其他非線性正箱體)，M1、M2兩面平行但不等寬，各側面上的高距為非線性變化，頂面為一非線性扭面。與線性扭面相比，此類方程較為複雜，而且難以直接求得，但若按照上述思路和方法使兩面間的縱、橫坐標單位數各自處處對應相等，便可先求出縱、橫兩個單向非線性變化方程之和，然後減去一個雙向線性變化方程，則該非線性扭面方程便不難求得。

上述線性和非線性扭面方程的基本思路和方法從根本上解決了各種扭面問題的精確表達（將自變數代入適當數值便可直接求得對應內插位置的精確函式值），以及各種有關的精確運算。若將常規直角坐標系運用上述思路和方法進行適當改進或擴展便可獲得箱變坐標系。

2.2、箱變坐標系的數學約定

箱變坐標系(因其最初來自正箱體而故名)與常規直角坐標系(笛卡兒坐標系)相比，二者既有相同之處也有本質上的不同。如圖5，二者的相同之處為：均有坐標原點、相互垂直的坐標軸和各自對應的坐標單位，也均有二軸平面坐標系和三軸空間坐標系等，即有三個基本要素相同。二者的根本不同在於第四要素，即同名坐標單位是否可變(變值)，由此決定了二者的坐標係數和坐標網形不同：常規直角坐標系的同名坐標單位處處相等(等值)，坐標係數或變值係數恆為常數1，故常規的直角坐標系(等值坐標系)可視為箱變坐標系的一種特例(這就如同10進制只是最常用的進位制一樣,常數1也只是最常用的坐標係數)，其坐標值可叫等值坐標，其坐標網為均勻的矩形平面網(矩形網)或直方體空間網(方體網，可有三個坐標平面所控制)；箱變(變值)坐標系的同名坐標單位在不同位置是可變的，其對應坐標可叫變值坐標，其坐標網也隨之不同。

箱變坐標系的坐標網可以某一標準正箱體為基準或原型(可叫基箱體)，按照等比對應或變值對應進行網狀分割而成(如圖5，圖中的基箱體為線性直次箱體，也可為其他標準正箱體)，分割後的平面圖形(對應於二軸箱面坐標系)常為直邊或曲邊的梯形網(如正箱體的側面)或任意四邊形(如次箱體的底面)，空間圖形(對應於三軸箱體坐標系)常為相應的正箱網(此時須由三組箱面所控制)，與基箱體對應的坐標網可叫基準網。在箱變坐標系中，基箱體的三個互垂側面稱為基準側面或基側面，與三個坐標平面相對應，另外的三個側面稱為變值側面或叫變側面，常用於確定坐標係數(用於坐標系中)或變值係數(用於函式式中)。當基箱體的三個共點互垂側面與三個坐標平面相互重合時(稱為最簡位置)，相應坐標系稱為最簡箱體坐標系；此時，與基側面對應的平面坐標系可叫最簡箱面坐標系(如圖5，a為b的OXZ坐標平面)。最簡箱體和箱面坐標系可統稱為最簡箱變坐標系或最簡坐標系。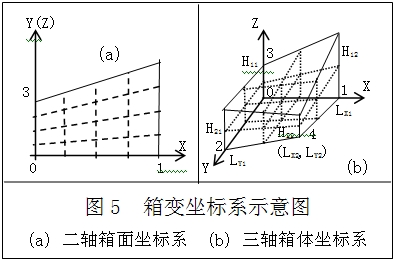

在箱變坐標系中，處處可變的坐標單位(叫變值單位)與某一基準單位(叫基值單位，常為其同名坐標軸上的坐標單位)之比叫坐標係數或變值係數(相當於坐標值自身的變化率),即：變值係數=變值單位/基值單位=變值坐標/基值坐標。亦即：變值坐標=基值坐標×變值係數，此式可叫變值公式，是進行坐標變換或坐標換算的算法依據。當變值係數為1時，則變值坐標=基值坐標=等值坐標。在通常情況下，近箱坐標系至少有一種同名坐標係數恆為1(如等長近箱體的縱向坐標係數，等寬近箱體的橫向坐標係數)；次箱坐標系的各種坐標係數全不為1；當各種坐標係數處處為1時，箱變坐標系變為等值坐標系。因此，箱變坐標系與等值坐標系的區別和聯繫依賴於變值係數。其中，長距和寬距係數的主要作用是將各類正箱體變換為同名坐標單位數處處相等的方箱體。

由上述可知,箱變坐標系應處於以其基值單位為坐標單位的等值坐標系中。因此,箱變坐標系應為一種包含直角等值坐標系的複合坐標系,而且便於進行不同坐標單位的相互變換。通常，某一點的坐標常用基值坐標表示[可用大寫字母表示，如(X,Y)]，也可用變值或等值坐標表示[可用小寫字母表示，如(x,y)]。在同一複合坐標系中，同一點位的變值坐標與等值坐標的坐標單位值和單位數雖然不同，但兩種坐標值應完全相同，亦即二者同位同值。

在最簡箱變坐標系(如圖5)中，基箱體在X軸上的寬距叫基寬(01)，在Y軸上的長距叫基長(02)，在Z軸上的高距叫基高(03)。這裡的基長、基寬和基高可統稱為基箱體的基距。各種基距均不能為0，否則應變換基側面求其基距。有時，基距也可根據需要適當設定(如變值合併的通基變換)。由於箱變坐標系的坐標網是對基箱體的等比對應或變值對應分割而成，故X、Y和Z的變值係數可分別叫寬距係數（=寬距/基寬)、長距係數（=長距/基長)和高距係數（=高距/基高)。這裡的長距、寬距和高距均可表示為截距不為0的某一初等函式，基長、基寬和基高等於各自對應函式的截距。在各種正箱坐標系中，長距和寬距係數均為一元，高距係數一般為二元，特殊情況也可為一元（此時的高距函式也應為一元）。

歸納上述，可得最簡箱變坐標系的三種基本對應(特性)：一為等基對應，即同一坐標網線或網面上的同名坐標基值(或基值坐標或坐標單位數)處處對應(相等)，不同坐標網線或網面上的同名坐標基值處處不等；二為變值對應，即基值相同的同名變值坐標處處對應(位於同一網線或網面上)，基值不同的變值坐標互不對應(不在同一網線或網面上)；三為等比對應，即任意兩個同位的變值坐標之比等於各自對應的基值坐標之比，反之依然(即兩個基值坐標之比等於各自對應的任意兩個同位變值坐標之比)。以上三種對應同樣適用於等值坐標系，只不過其坐標基值與其變值相同而已。

此外，若將坐標單位值視為質量或密度，則等值坐標系可對應於均質或均勻空間，箱變坐標系可對應於非均質或非均勻空間，而前者又可視為後者的特殊情形。從坐標網線來看，等值坐標系對應於靜態的線性無限空間，箱變坐標系可擴展到動態的非線性有限到無限空間（後者包含了前者）。進而，便可實現各種物理空間與各種數學空間的相互對應。

以上對正箱坐標系的有關說明也同樣適用於斜箱坐標系(其基箱體應為標準斜箱體)。斜箱坐標系的變值係數仍然是將其基箱體變為坐標單位數對應相同的方箱體，但由於其有關算式和最簡變換較為複雜，其有關算法(如積分運算等)還不成熟,尚無用於CS法,故不詳述。

2.3、箱變坐標系的建立方法

這裡重點說明最簡坐標系。此時，可先建立笛卡兒坐標系，然後求出其坐標係數並做好標註即可。這裡的關鍵是如何求出坐標係數，通常可有設定法和基箱法兩種求法。設定法(無基箱體時)可根據實際需要直接將坐標係數設定為首項為1的某一連續型初等函式，此時，任取一組基距便可獲得與之對應的某一基箱體；基箱法(有基箱體時)通常是將某一基箱體的基側面與笛卡兒坐標平面相互重合(屬最簡位置)，並求出其長距、寬距和高距的函式式(即各自對應的變側面方程)，然後除以同名基距(亦即各自對應函式的截距，不能為0)而得相應變值係數(用K表示，首項為1)。此時的截距為基值坐標，函式式為其對應的變值坐標。基箱法的一般步驟是：首先求出基箱體的各種變側面和變距方程，然後除以各自的對應基距即可。

採用基箱法建立最簡（標準）坐標系時，應做到三重合三對應(箱面坐標系應為二重合二對應)。三重合常為：XOZ平面與1號橫側面重合，YOZ平面與1號縱側面重合，XOY平面與底面重合；三對應常為：Y坐標(也可為X或Z)與長距(縱向)對應，X坐標(也可為Y或Z)與寬距(橫向)對應，Z坐標(也可為X或Y)與高距(箱高)對應。其中的Y(長距)和X(寬距)坐標，在近箱體中只有一種為變值坐標，另一種為等值坐標；在次箱體中兩種均為變值坐標；Z(高距)坐標則既可為變值坐標也可為等值坐標(基箱體等高時)。由於箱變坐標系的坐標係數也是可變的，故可將其視為不均勻的動態坐標系。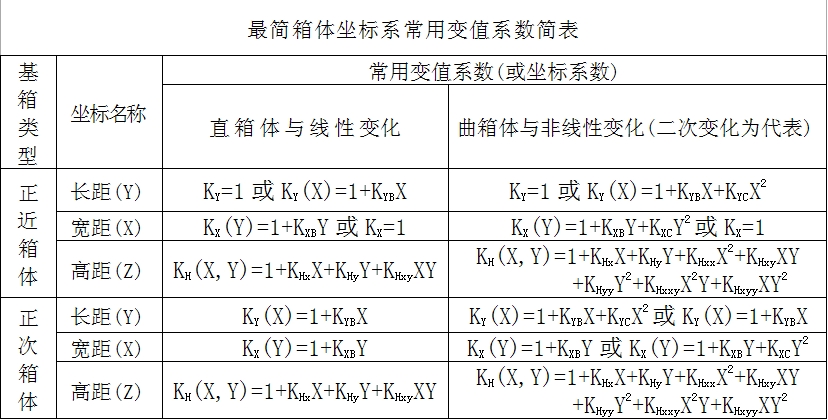

各種變值坐標系提示

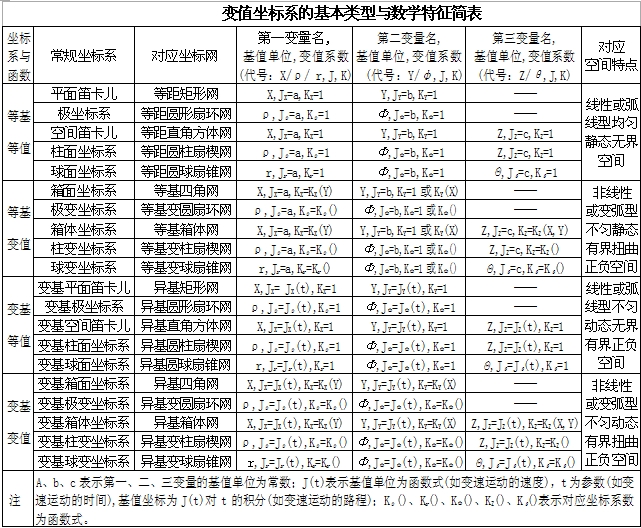
在現代數學中，比較常用的常規坐標系可有五種（圖6），而上述箱變坐標系只是對常規直角坐標系的初步擴展，此時可叫等基方法(包括等基等值和等基變值，其中的“等基”是指同名基值單位處處相等，可視為勻速運動的速度，對應基值坐標則為勻速運動的距離)，若再進一步擴展可得變基方法(包括變基等值和變基變值，其中的“變基”是指同名基值單位處處可變，可視為變速運動的速度，對應基值坐標則為變速運動的距離)。進而若將其它幾種常規坐標系(如極坐標系、柱面坐標系和球面坐標系等)和相應函式也進行同樣擴展便可構成一套比較完整的變值坐標系、變值函式和變值運算等變值方法（即CS變值方法）。其中，與五種常規坐標系相對應的各種變值坐標系可有20種組合，其基本特徵列於下表，供參考。