系統的諸因素中含有不能用確定的量進行描述的系統或呈現有不確定性信息的系統稱為不確定性系統。所謂不確定，即不明確、不肯定。不確定的量是表述系統中不確定性信息的量，如模糊量、灰色量，都是不確定的量，分別稱之為模糊不確定量、灰色不確定量。
不確定性系統預測的基本出發點是強調以系統思想為指導，以綜合處理不確定性信息為主要手段。它沒有改變經典預測的初衷，是經典預測的繼承和發展。因此，經典預測理論的基本原理在此仍具有指導作用。
基本介紹
- 中文名：不確定性系統
- 外文名：Uncertainty system
- 含義：指一個事件的未來結果不止一種
- 分類：3類
- 出發點：以系統思想為指導
內涵與外延,理論框架,系統特性,研究思路,
內涵與外延
關於 “系統” 一詞 , 有著各種不同的定義。 《灰色系統理論的數學方法及其套用》中曾把系統定義為: “由若干個 (≥ 2) 相互關聯、 相互制約的元素組成的具有某種特定功能的整體。”不論哪一個定義 , 其中都有 “相互作用的若干元素的整體” 之意。 如果拋開人的因素 , 可以說宇宙間任何可以獨立的整體都具備這一條 , 都可視為系統 , 我們稱之為自然系統。 如果把人的因素考慮進去 , 就有一個主觀上的 “功能” 和 “目的” 問題。 人類要認識系統的性能 , 改造並利用系統 , 使之服務於人類。我們把加入人為因素的自然系統稱為複合系統。 另外 , 人類為了某種需要而構造某種系統 , 我們稱之為人為系統。
《灰色系統理論的數學方法及其套用》中從另一角度定義說: “系統的諸因素可以用確定的量來描述的系統叫作確定性系統;系統的諸因素中含有不能用確定的量進行描述的系統叫不確定性系統。”人為系統 , 其諸因素的技術參數皆為人類設計給定的 , 是確定的量 , 故人為系統在未運行之前可以視為確定性系統。複合系統是有人參與的自然系統。 其諸因素的量化值皆由人觀測所得。 由於系統的複雜性、 外界噪音的干擾以及人類觀測能力的限制 , 人類不可能獲取確切的量化值。 故複合系統是不確定性系統。 自然系統 , 因為它是客觀上存在的系統 , 在無人參與的情況下 , 其結構、 性能是本身所固有的 , 是確定性系統。 一旦有人參與 , 它便是複合系統 , 亦即是不確定性系統。可見 , 不確定性系統的外延是極為廣泛的 , 除個別的人為地認為是確定性系統外 , 皆為不確定性系統。 不確定性系統的研究方法是亟待解決的問題。
我們又稱 “呈現有不確定性信息的系統為不確定性系統。”因為不確定性信息的量化結果必為不確定的量。 故兩種定義在內涵上是一致的。
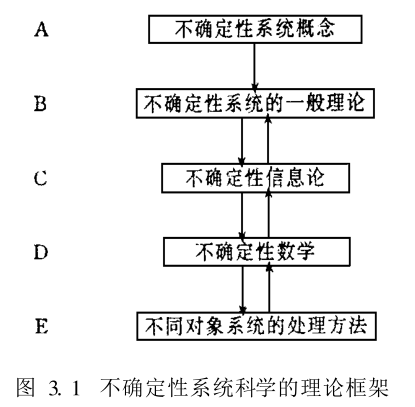
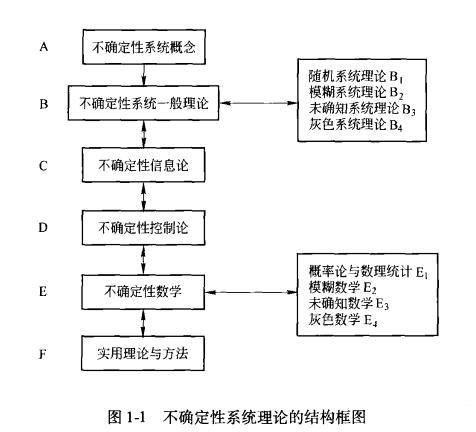
理論框架
我們稱研究不確定性系統的理論為不確定性系統理論 ; 稱以不確定性系統為對象的科學為不確定性系統科學。 其理論框架如圖 3. 1所示。
A級是不確定性系統科學的研究對象— 不確定性系統。 它包括四個子系統: 隨機系統 ( RandomSystems ), 模糊系統 ( Fuzzy Systems ) , 灰色系統( Grey Systems ),未確知系統 ( Unascertained Sys-tems)。
B級是關於不確定性系統科學一般性理論。它不是關於某種特殊的不確定性系統的理論。 而是適於各種不確定性系統的普遍原理 , 把各種不確定性系統的共性和異性抽象出來形成理論的客體。 它包括四個子客體: 隨機系統理論 , 模糊系統理論 , 灰色系統理論 , 未確知系統理論。
C 級是關於不確定性信息共性理論 , 是不確定性系統科學的核心。
我們的時代正走向信息化時代; 然而資訊理論落後於時代的情況實在太嚴重了。雖然 Shannon 資訊理論已經名聲卓著 , 但它所涉及的信息僅僅是日常語言所說的信息的一小部分 , 即被減少了的不確定性。 而對語義信息、 感覺信息、 偶然事件及測量數據所提供的信息是無能為力的。更進一步地說 , 它對模糊信息、 灰色信息、 未確知信息是無能為力的。 在 Shannon資訊理論誕生不久 , 有人把它用在日常信息交流場合 , 結果漏洞百出。為此 , Shannon 非常憤慨 , 並措辭嚴厲地給予指責;要求人們對他的理論的套用不要超出隨機統計領域。 這表明 , Shannon資訊理論是有一定局限性的。我們有必要在繼承的基礎上發展它。 而且 , 在上面的討論中我們已經發現 , 不確定性信息的產生是不可避免的。 因此 , 我們提出建立不確定性資訊理論是非常必要的、 適時的。
D 級是不確定性系統科學的基礎。因為沒有相應的數學理論和方法就不能合理地處理不確定性信息進而解決系統問題 , 就不能實現計算機模擬。這裡要強調的是 , 我們不僅要注重四種不確定性數學分支的發展問題 , 更要注意綜合處理各種不確定性信息的不確定性數學的建立和發展問題。
E級是理論與實踐相結合的一級。因為凡有人參與的系統皆為不確定性系統 (特別是經濟系統 )。所以 , 套用不確定性系統科學理論和方法研究對象系統最佳化問題是大有文章可做的。
系統特性
系統思想,可以說自有人類社會以來就一直在孕育發展著。公元 5世紀左右，西方著名代表人物徳漠克利特就寫過一本名為《宇宙大系統》的著作，我國的《易經》、《老子》也包含了豐滿的系統思想。中醫的 整體思想，至今還為現代西方醫學所不及。但由於歷史的原因,作為科 學的系統概念和一般系統理論的歷史卻相當短。它是第二次是世界大戰 前由路德維希·馮·倍塔朗菲（Ludwig Von Bealamffy)提出的，到1954 年建立一般系統理論促進會後,才被人們普遍了解。自此以後,系統理 論得到迅猛發展，並在工程系統和科學管理中得到廣泛套用，形成了經 典系統理論。近幾十年來，隨著人們對不確定性信息認識的深入，越來 越感到經典系統理論已不能滿足社會發展的需要。但它的基本思想仍 然存著它的深遠意義。
不確定性系統的基本特性有：
(1)整體性。系統是由若干個不同要素組成的有機整體,不是簡 單的集合。它的結構、功能、可操作性以及運行狀態只有作為整體才能 得以充分體現，離開了整體，任何一個元素，不論它是多么重要的元素, 都將失去它的應冇作用。作為反映系統本質屬性的信息同樣具有系統 的整體性，黑、白信息之總和，一定是系統整體信息之總和;確定性信息與不確定性信息之總和，一定是系統整體信息之總和。
(2)相關性。系統各要素之間是有機聯繫的、相互作用的，任何一 個要素的功能的發揮都離不開其他若干要素的支持;任何一個要素的 作用都將支持其他要素功能的發揮;任何一個元素都不可能獨立地發 揮其作用，也不可能獨立地影響系統整體功能的發揮。作為反映系統 的信息也是如此,它們不可能獨立地由源信息轉化為宿信息，它們是有 機地表露的。因此，通過各種信息的關係可以認識系統各元素的性能 及其相互聯繫。
(3)環境適應性。任何一個系統都處在一個特定的環境之中，它 必須適應外部環境的變化才能立足於客觀世界,才能發揮它應有的作 用。源信息在向宿信息轉化的過程中，外界環境會影響它的本質特性 的表露。因此，我們在分析處理信息的過程中，要時刻考慮外界噪聲的 影響，分清信息的類別，通過處理後的信息反饋，以保證系統環境適應 性的發揮。
研究思路
不確定性系統的研究思路：
因為不確定性系統是呈現有不確定性信息的系統，而對確定性信 息在經典系統理論中已有了廣泛研究,故研究不確定性系統，關鍵是研 究不確定性信息的處理方法。
目前，人們已經認識到了四種不確定性信息：隨機信息、模糊信息、 灰色信息、未確知信息，而且有了各自的處理方法。研究處理隨機信息 的方法是機率論、數理統計、隨機過程。研究處理模糊信息的方法是模 糊系統理論和模糊數學。研究處理未確知信息的方法是未確知數學。 研究處理灰色信息的方法是灰色系統理論和灰色數學。在某類系統 中，由於各種不確定性信息表現得特別突出，從而採用某種不確定性信 息的處理方法，在一定程度上是可行的。
在《不確定性數學及其研究方向》中指出：“在一個系統中，各種 不確定性信息有時交叉呈現，有時同時呈現。” 因此，要理想地研究不 確定性系統的功能和運行控制，單獨考慮某一種不確定性信息的處理 是不全面的。於是在此文中又提出“綜合處理不確定性信息”的問題。 而且把“綜合處理不確定性信息的數學理論與方法”定義為不確定性 數學。關於綜合處理不確定性信息問題，我們考慮了兩條路線：
第一，因為灰色信息的特徵是:部分信息已知,部分信息未知。已 知的信息視為“白”，未知的信息視為“黑”。因為部分已知的白信息 中，必然包含有隨機信息、模糊信息或未確知信息。在“Mathematical Relations among Four Kinds of Uncertainties” 一文中已論證了這一 結論。所以，可以在灰色系統理論的思想指導下，套用泛灰色數學 方法實現對各種信息的綜合處理。
第二，因為人類主體向客體提取信息的過程是人類通過主體標度 對客體進行測量的過程。客體中的因素、特性與標度之間的關係只有 同一、對立和差異三種情況。同一性與對立性表現為確定性，差異性表 現為不確定性。根據系統的整體性原理，確定性在系統中的比例或程 度確定之後，不確定性在系統中的比例或程度也就相應地確定下來了。 在這裡，不區分是哪一種不確定性，它是各種不確定性的綜合表 現。對這些關於不同系統的不確定性的表現程度進行分析運符，便可 實現各類信息的綜合處理。
