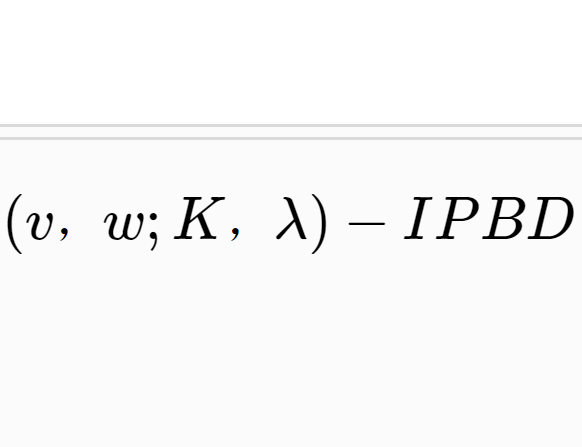不完全成對平衡設計(incomplete pairwise balanced design)是帶子設計的成對平衡設計(PBD設計)的推廣，設X為v元集，Y為X的w元子集，A是X的某些子集(稱為區組)的族，A中區組的大小均在某個正整數集合K中，若當X中的任意兩個元均屬於Y時它們不含於任何區組，否則它們恰含於λ個區組，則稱(X，Y，A)為一個不完全成對平衡設計，記為(v，w;K，λ)-IPBD。
基本介紹
- 中文名：不完全成對平衡設計
- 外文名：incomplete pairwisebalanceddesign
- 所屬學科：數學（組合學）
- 簡介：帶子設計的PBD的推廣
基本介紹,相關介紹,
基本介紹
若集Y上存在一個
，則
是一個帶子設計的PBD，但是，集Y上未必存在這樣的子設計，所以，IPBD的概念比帶子設計的PBD更為一般，在PBD的遞推構造中有時需要比IPBD更一般的概念，設X為v元集，Y1與Y2分別為X的ω1及ω2元子集，
，A是X的某些子集(稱為區組)的族，A中區組的大小均在某個正整數集合K中，若當X中的任意兩個元均屬於Y1或均屬於Y2時它們不含於任何區組，否則它們恰含於λ個區組，則稱
為一個格子不完全成對平衡設計，記為
相關介紹
成對平衡設計(pairwise balanced design；PBD設計)是的平衡不完全區組設計一種推廣，設X為v元集，B是X的某些子集(稱為區組)的族，B中區組的大小(數)均在某個正整數集合K中，若X的任意兩個元素恰含於B的λ個區組中，則將二元組(X，B)稱為成對平衡設計，記為
，當區組大小都相同時，這種特殊的成對平衡設計就是平衡不完全區組設計。
定義設v與λ為給定的正整數，K為給定的正整數集合，又設D=(V，B)為有限關聯結構，若以下條件滿足：
(i)|V|=v；
(ii)對任意B∈B。都有|B|∈K；
(iii)V中任意一對不同的點都恰好同時包含在λ個區組中，
則稱D為一個成對平衡設計(pairwise balanced design)。簡稱PBD設計。記作
，v叫做設計的階。λ叫做相遇數。
PBD設計是BIB設計的自然推廣。當K={k}時。
就是BIB設計B(k，λ；v)。
設D=(V，B)為一個。若存在區組B∈B使
。則稱D為非退化的PBD設計。
需要指出的是，對某個k∈K。B可能不包含容量為k的區組，因此當K1⊆K2為兩個正整數集時。每一個B(K1，λ；v)也可看作一個B(K2，λ；v)。
成對平衡設計的概念和方法曾對正交拉丁方及平衡不完全區組設計的存在性和構造方法的研究起過重要的作用.例如，玻色(R.C.Bose)等關於歐拉猜想的反證，哈拿匿(H.Hanani)關於區組大小為3，4，5的平衡不完全區組設計存在的充分必要條件，以及哈拿匿等關於區組大小為3，4的可分解平衡不完全區組設計存在的充分必要條件等，在這些重要的工作中，成對平衡設計作為研究組合設計的一般工具也得到了發展，威爾森(R.M.Wilson)於20世紀70年代引入了PBD閉集的概念，在此基礎上形成的PBD閉集方法不僅簡化了一些經典結果的證明，也為統一處理新提出的各種組合設計的存在性問題提供了有效的途徑，若
