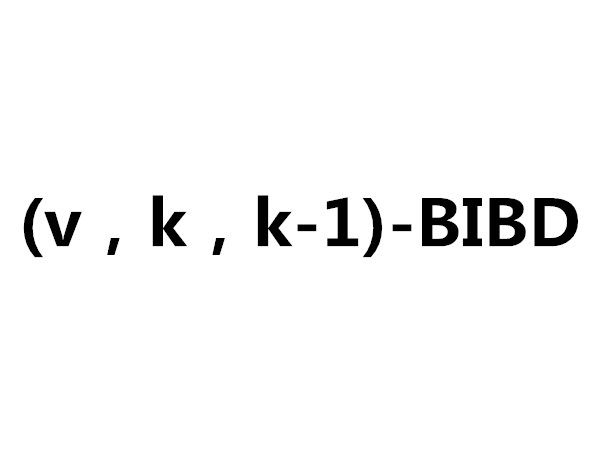準可分解設計(almost resolvable design)是可分解平衡不完全區組設計的一種變體,設(X,B)是一個(v,k,k-1)-BIBD,v≡1(mod k),若區組族B有一個劃分B1,B2,…,Bv,使得對每個Bi,存在點x,使Bi是X\{x}的劃分,則稱這個BIBD設計為準可分解設計。
基本介紹
- 中文名:準可分解設計
- 外文名:almost resolvable design
- 所屬學科:數學
- 所屬問題:組合學(組合設計)
- 簡介:RBIBD設計的一種變體
基本介紹,相關概念,
基本介紹
對於準可分解設計,當k=3,4時,準可分解設計的存在性已經解決,只要v≡1(mod k),總存在準可分解的(v,k,k-1)-BIBD,關於k=5的準可分解設計的存在性,目前僅剩有限個v值尚未確定。
相關概念
區組設計
區組設計是組合設計研究的主要對象之一,設有限集X含v個元素x1,x2,…,xv,這些元素稱為點或處理.B1,B2,…,Bb是X的b個子集(其中可能有相同者),這些子集稱為區組,將這些區組組成的子集族記為B,稱對子(X,B)為一個區組設計,這樣定義的區組設計並不包含多少信息,為在理論研究和實際套用中得到有意義的對象,需要對區組設計加強條件,當(X,B)中有兩個區組相同時,稱它們為重複區組,無重複區組的設計稱為簡單設計.在一個區組設計中,若每個點恰在r個區組中出現,且每個區組恰包含k個點,則稱該區組設計為正則設計,稱r為重複數,k為區組大小.當區組設計中任意兩個不同的點恰好同時出現在λ個區組中時,稱該區組設計為平衡設計,且稱λ為設計的相遇數.區組B與X相同時稱B為完全區組.若區組設計中至少有一個區組不是完全區組,則稱之為不完全區組設計.當B中有一部分區組形成集X的一個劃分時,稱這部分區組為一個平行類.若B可以劃分為若干個平行類,則稱該區組設計是可分解的.組合設計的基本問題之一是研究各種區組設計存在的充分必要條件。
可分解平衡不完全區組
可分解平衡不完全區組設計是一類特殊的BIBD設計,縮寫為RBIBD。即其區組全體可以劃分為一些平行類的BIBD設計,一個參數為(v,k,λ)的可分解BIBD設計記為(v,k,λ)-RBIBD.一個(v,3,1)-RBIBD也稱為柯克曼三元系.它的存在性直到1971年才由雷·喬德里(Ray-Chaudhuri,D.K.)和威爾森(Wilson,R.M.)徹底解決.他們證明:(v,3,1)-RBIBD存在的充分必要條件為v≡3(mod 6).接著他們與哈拿匿(Hanani,H.)一起證明:(v,4,1)-RBIBD存在的充分必要條件為v≡4(mod 12).與此同時,前兩位作者還猜測v≡5 (mod 20)是(v,5,1)-RBIBD存在的充分必要條件.目前除5個可能例外的v值(最小為45,最大為645),這個猜測已被證實.與BIBD設計相類似,可分解BIBD設計的存在性也已有了漸近結果,雷·喬德里和威爾森證明了λ=1的情形,中國的陸家羲把λ推廣為一般的情形.他們證明:對給定的正整數k和λ,除有限多個正整數v外,(v,k,λ)-RBIBD存在的充分必要條件是v≡0(mod k)和λ(v-1)≡0(mod k-1).這裡的“有限多個正整數v”並沒有明確給出究竟有多少,這是有待進一步解決的問題.關於RBIBD,玻色(Bose,R.C.)於1942年證明了不等式:b≥v+r-1.當等號成立時,稱該設計為仿射的,記為ARBIBD(參見“仿射可分解設計”)。
仿射可分解設計
仿射可分解設計是一類特殊的可分解區組設計,當一個可分解區組設計中任意兩個不在同一個平行類中的區組都恰好有m個公共點時,稱這個區組設計是仿射可分解設計,仿射可分解設計必定是一個可分解BIBD設計.玻色(Bose,R.C.)證明:若且唯若一個可分解BIBD設計的參數滿足b=v+r-1時是仿射可分解的,金勃萊(Kimberley,M.E.)於1971年證明:一個3設計是仿射可分解的充分必要條件是它是一個擴充阿達馬2設計,且當t≥4時,沒有仿射可分解的t設計.從仿射可分解的BIBD設計可以得到一類對稱設計.沃利斯(Wallis,W.D.)證明:若存在仿射可分解(v,b,r,k,λ)-BIBD,則存在(v′,k′,λ′)-SBIBD,其中v′=(r+1)v,k′=kr,λ′=kλ.仿射可分解設計後來被推廣為仿射α可分解設計.一個α可分解設計的區組族按定義分成組B1,B2,…,Bt後,若同一組中的任兩個區組有q1個公共點,不同組中的任兩個區組有q2個公共點,則稱為仿射α可分解設計。