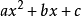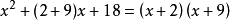三項式

三項式是指初等代數中項數為3的多項式，即三個單項式相加的和。

基本介紹

• 中文名：三項式
• 外文名：Tri-equation
• 拼音：Sān xiàng shì
• 學科：數學
• 隸屬：多項式
• 概述：項數為3的多項式

基礎內容

在數學中，由若干個單項式相加組成的代數式叫做多項式。多項式中的每個單項式叫做多項式的項，這些單項式中的最高項次數，就是這個多項式的次數。其中多項式中不含字母的項叫做常數項。

三項式是三個項組成的多項式，最常見的形式是二次三項式 。不過不是所有三項式都是二次的，有的還有更高次數。

平方和立方公式

三項式平方公式： ；

三項式立方公式： 。

示例1：求三項式a-2b+1的平方。

解： 。

因式分解

多項式在數學和科學中都很有用，學好因式分解多項式的方法，可以在很多領域中得心應手。下面介紹因式分解三項式的基礎方法。

1. 把三項式中三項的公因子提出來。如果三個項係數都有相同因數，提出來；或者含有共同變數，也提出來。再把三項式參數按從大到小次數排列。參數是多項式中的變數，正常順序就是按次數大到小來排列的。
2. 把三項式分解成兩個二項式因式。二項式是含有兩個組成部分的mx +n形式的多項式，m、n代表常數。兩個二項式中的首項應該是三次項(ax)的因數，二項式的第二項應該是三項式中常數(c)的因數。把第一個多項式首項和第二個多項式的次項相乘，然後把第二個多項式首項和第一個多項式的次項相乘就得到三次多項式的(bx)。
3. 看看三項式是否是完全平方式。完全平方式是一個項自己乘自己得到的式子。如果是完全平方式，a 和 c一定是完全平方，b一定是 a 和 c的根的和的兩倍。

示例2：對下列二次三項式進行因式分解。

解： ； 。

次數計算

多項式的次數是指多項式中最高單項式的次數。三項式是多項式中的一種，所以方法相同。三項式的次數計算要看未知數的最高次項的次數。

示例3： 是五次三項式（未知數的最高次數是5，有3項）； 是三次三項式（未知數的最高次數是3，有3項）。

教學套用

在三項式的數學教學中可以採用“探究法”。“探究法”的精髓在於以學生為主角，使他們由被動地接受知識轉變為知識的探索者。通過親自動手，積極思考，熱烈討論，探索知識，學生能更加深入理解知識的內涵，並培養觀察力、思維能力、動手能力、歸納能力、語言表達能力和創造能力等。“探究式教學法 ”是指在老師的指導下 ，學生通過具體的操作，親自嘗試後，經過積極思考和討論，找到知識的規律，總結出結論，學會新知，並發展思維、培養能力的綜合教學方法。通過讓學生對多項式的內容進行了解，可以引導學生對三項式這一知識點進行積極思考。從中拓展學生思維、提高學生獨立思考的能力。