基本介紹
- 中文名:三角方程組
- 外文名:system of trigonometric equations
- 所屬學科:數學
- 所屬問題:代數與方程(三角方程)
- 簡介:含有三角方程的方程組
三角函式方程組的解法原理
解三角方程組的注意事項





例題解析























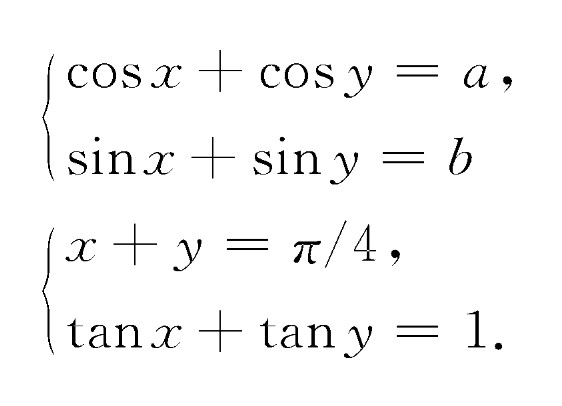




























所謂三角方程組(system of trigonometric equations)是指方程組中或僅僅包含三角方程,或包含三角方程和代數方程。如果一個未知數能表示為另一個未知數的顯式,那么可將三角方程組化為含單變數的一個...
完全三角形方程組是一種特殊的線性方程組。係數矩陣是對角元素全不為零的上(下)三角方陣的線性方程組叫做完全上(下)三角形方程組,簡稱完全三角形方程組。完全三角形方程組有唯一解。簡介 完全三角形方程組是一種特殊的線性方程組。形如 的方程組稱為完全三角形方程組,其中對角線上的係數a,a,...,a都不...
混合三角方程(mixed trigonometric equation)是一種三角方程,指未知數不全含在三角函式記號下的方程。例如tan x -3x=0。三角方程可分成兩類:純三角方程和混合三角方程,若未知數隻出現在三角函式符號下,叫做純三角方程,例如2sin²x+3cosx=0。混合三角方程的解法與舉例 混合三角方程只能用圖解法或疊代法來求解...
若能通過正交變換,將係數矩陣A分解為A=LU,其中L是單位下三角矩陣(主對角線元素為1的下三角矩陣),而U是上三角矩陣,則線性方程組Ax=b變為LUx=b,若令Ux=y,則線性方程組Ax=b的求解分為兩個三角方程組的求解:(1)求解Ly=b,得y;(2)再求解Ux=y,即得方程組的解x;因此三角分解法的關鍵問題在於係數...
反三角方程組(system of inverse trigonometric equations)是一種特殊方程組,指含有反三角方程的方程組。同時滿足反三角方程組中每個方程的公共解,稱為反三角方程組的解。求解反三角方程組的過程,稱為解反三角方程組。基本介紹 反三角方程組指含有反三角方程的方程組。例如方程組 為反三角方程組,因為其中有反...
常微分方程,屬數學概念。學過中學數學的人對於方程是比較熟悉的;在初等數學中就有各種各樣的方程,比如線性方程、二次方程、高次方程、指數方程、對數方程、三角方程和方程組等等。這些方程都是要把研究的問題中的已知數和未知數之間的關係找出來,列出包含一個未知數或幾個未知數的一個或者多個方程式,然後取求...
非線性方程組數值解法 - 布朗方法 布朗採用對每個分量方程 ƒi(尣)=0逐個進行線性化並逐個消元的步驟,即在每疊代步中用三角分解求線性方程組的解,得到了一個效率比牛頓法提高近一倍的疊代法,即 式中 (8)中當i=n時求得xn記作 ,再逐次回代,求出 (i=n-1,n-2,…,1)就完成了一個疊代步。布朗疊代...
喬萊斯基分解法(Cholesky decompositionmethod)亦稱平方根法.解對稱正定線性方程組的常用方法之一設線性方程組A二一b的係數矩陣A是n階對稱正定矩陣.喬萊斯基分解法是先求A的分解A=LLT,其中1為對角元均為正數的下三角矩陣,其元素乙,可由下面的公式遞推計算:然後再依次解兩個三角形方程組LTy=b和1.x =y,從而...
解稀疏線性方程組的方法包括直接法(direct method)與疊代(iterative method)兩類。直接法指在不考慮計算捨入誤差的情況下,通過包括矩陣分解和三角方程組求解等有限步的操作求得方程組的精確解,因此又稱精確法;疊代法指給定一個初始解向量,通過一定的計算構造一個向量列(一般通過逐次疊代得到一系列逼近精確值的近似...
吉文斯法(Givens method)是正交分解法的一種。它線上性方程組Ax=b的兩邊施行一系列吉文斯變換將其變為等價的上三角方程組,然後求解上三角方程組而得到原方程組的解。這一方法的運算是豪斯霍爾德法的兩倍,但吉文斯法有較大的靈活性,特別當係數矩陣A有較多的零元素時,適當安排吉文斯變換的次序可使運算量大為減少...
回代過程(back substitution process)指順序高斯消元法的一個主要步驟,順序高斯消去法是求解線性方程組的一種方法,主要包含消元和回代兩個過程。利用加減消元法將一般方程組式化為係數矩陣為上三角矩陣的上三角形方程組式的過程稱為消元過程,依次求出xx... ,xₙ稱為回代過程。定義介紹 設有線性方程組 或...
2.3 矩陣的LDLT分解和對稱方程組的求解 2.4 不可約對角占優矩陣以及三角方程組的求解 習題 第三章 方程組的條件和不相容方程組求解 3.1 向量和矩陣的範數 3.2 誤差分析和方程組的條件 3.3 不相容方程組的最小二乘解 習題 第四章 解線性方程組的疊代法 4.1 JACOBI疊代法的SEIDEL疊代法 4.2 線性方程...
矩陣的正交分解是指A分解為一個正交矩陣Q和一個對角可逆上三角矩陣R的乘積。矩陣正交分解的套用 正交分解是先將線性方程組Ax=b的係數矩陣A分解為一個正交矩陣Q和一個對角可逆上三角矩陣R的乘積。然後通過求解上三角方程組Rx=Qb而求得原方程組的解,這種方法一般比三角分解法運算量大,但數值穩定性較好。弧形的...
(ii)關於sinx、cosx的齊次方程(726―730)(iii)換元法(731―748)(3)因式分解法(749―780)(4)輔助角法(781―789)(5) 解三角方程的其它方法(790―805)(6)含參數的三角方程解的討論(806―827)§2.三角方程組(828―854)§3.三角不等式 (1)最簡三角不等式(855―861)(2)一般...
是上三角矩陣,則Ax=b化為一個同解上三角方程組,套用回代法即可求得方程組的解。部分主元高斯消去法的工作量約為 個浮點運算和 次邏輯運算。也可以用矩陣運算表示部分主元高斯消去法的消元過程。交換單位矩陣 I 的第 i ,j(i < j)兩行(列)所得的矩陣被稱為初等置換矩陣,記為 ,簡記為 ,...
1.1 三角形方程組 1.2 消元過程 1.3 Doolittle 分解和 Crout 分解 S2 主元消去法 2.1 主元素及選擇方式 2.2 帶行交換的矩陣三角分解 S3 消元法的誤差分析 3.1 LU 分解的誤差分析 3.2 誤差矩E的估計 3.3 解三角形方程組的誤差分析 S4 解正定對稱線性方程組的平方根法 S5 解三對角和帶狀線性方程...
2.6 正方形方程組的敏感性 2.7 有限精度矩陣計算 第3章 一般線性方程組 3.1 三角方程組 3.2 LU 分解 3.3 高斯消去法的捨入誤差 3.4 選主元法 3.5 改進與精度估計 3.6 並行 LU 分解 第4章 特殊線性方程組 4.1 對角占優與對稱性 4.2 正定方程組 4.3 帶狀方程組 4.4 對稱不定...
2.7 正方形線性方程組的敏感性 69 第3章 一般線性方程組 76 3.1 三角方程組 76 3.2 LU分解 81 3.3 高斯消去法的捨入誤差分析 91 3.4 選主元法 94 3.5 改進與精度估計 107 第4章 特殊線性方程組 116 4.1 LDMT和LDLT分解 118 4.2 正定方程組 122 4.3 帶狀方程組 133 4....
