該定理從老版高中教材人教版《數學》必修第二冊(下A),P35的例1:“河堤斜面與水平面所成的二面角為60°,堤面上有一條直道CD,它與堤腳水平線AB的夾角為30°,沿這條直道從堤腳向上行走10m時人升高了多少?”抽象出來的一般結論。
基本介紹
- 中文名:三正弦定理
- 表達式:sinγ=sinα·sinβ
- 套用學科:數學
- 適用領域範圍:立體幾何
定理概述,定理證明,定理套用,參見,
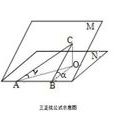
該定理從老版高中教材人教版《數學》必修第二冊(下A),P35的例1:“河堤斜面與水平面所成的二面角為60°,堤面上有一條直道CD,它與堤腳水平線AB的夾角為30°,沿這條直道從堤腳向上行走10m時人升高了多少?”抽象出來的一般結論。
三正弦定理編輯 鎖定 討論999 該定理從老版高中教材人教版《數學》必修第二冊(下A),P35的例1:“河堤斜面與水平面所成的二面角為60°,堤面上有一條直道CD,...
文字敘述為:三面角中任一二面角的餘弦值,等於其所對面角的餘弦減去另兩個面角的餘弦之積,再除以這兩個面角的正弦之積。 根據這個定理,結合三正弦定理就可以求直...
三正弦定理三餘弦定理最小角定理射影面積定理射影長定理祖暅原理詞條標籤: 科學, 學科 圖集 幾何定理圖冊 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:48次...
註明:摺疊角公式以及三正弦定理的套用為立體幾何的解題帶來了許多方便。摺疊角公式公式特點 編輯 輔助記憶:這三個角中,∠COB是最大的,其餘弦值最小,等於另外兩個...
