一致概周期微分方程(uniformly almost peri-odic differential equation)概周期常微分方程研究的主要對象
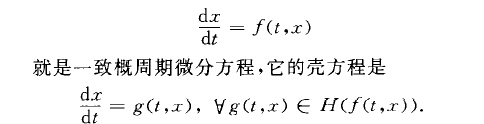

一致概周期微分方程(uniformly almost peri-odic differential equation)概周期常微分方程研究的主要對象
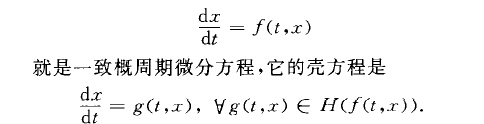

一致概周期微分方程(uniformly almost peri-odic differential equation)概周期常微分方程研究的主要對象.設.f(t,x)EC(RXD,R"),f對xED是一致概周期函式.那么...
方程說明 其右端函式對自變數是概周期函式的微分方程;即在方程 (1)中,?(x,t)是t的概周期函式。這裡x是n維向量,?(x,t)是n維向量函式。概周期微分方程的發展歷史不長,但由於它具有實際背景(如天體力學和非線性振動的問題)而顯示...
概周期常微分方程(almost periodic ordinarydifferential equations)常微分方程的一個重要分支.在自然與社會現實中概周期現象是比周期現象更為普遍存在的現象.例如,在經濟學、生態學、振動理論、電力系統以及天體力學等許多學科領域出現線性或...
《概周期微分方程及一些相關問題》是依託北京師範大學,由袁榮擔任項目負責人的面上項目。項目摘要 自然科學與社會科學中的很多實際問題都可歸結為概周期微分方程的研究。本項目將在理論上研究幾類受廣泛關注的微分方程的運動的變化規律,...
《逐段常變數微分方程的概周期型解》是依託哈爾濱理工大學,由姚慧麗擔任項目負責人的數學天元基金項目。項目摘要 本項目主要研究概周期型函式空間中的漸近概周期函式(AAP)和偽概周期函式(PAP),尋找研究AAP和PAP的一些性質的一般方法...
《二階微分方程解的概自守性》是依託華中師範大學,由張俊擔任項目負責人的數學天元基金項目。項目摘要 概自守函式和偽概自守函式是概周期函式的發展與延伸。概自守函式對於函式的一致連續性要求比概周期函式要弱,從而能夠更準確地反映實際...
如果一致概周期微分方程 的解 φ(x) 相對於其他解具有性質 P ,若 , 而ψ(t) 相對於 的解也具有性質 P ,則稱性質 P 是可繼承的。也就是說,若解φ(x)具有可繼承的性質 P ,那么,性質 P 在運算元 T的作用下是自封的。
可繼承性(inherited property)關於一致概周期微分方程解的一種重要性質.如果一致概周期微朴卞程 的解也具有性質屍,則稱性質屍是可繼承的.也就是說,若解抓t>具有可繼承的性質屍,那么,性質屍在運算元T。的作用下是自封的.通常往往...
與解和方程無關.半分離性質的可繼承性對保證概周期解的存在性起著重要作用.如果一致概周期微分方程僅有有限個在K內具有性質屍的解,又性質屍是半分離和可繼承的,那么,每個這樣的解在R一上是漸近概周期的,從而在K內有概周期解.
林振聲寫有40餘篇論文、專著有《概周期微分方程與積分流形》,《線性系統指數型二分性與雙曲結構》,及與楊信安教授合著的《微分方程穩定性理論》。1978年獲福建省高校科技成果一等獎,1990年獲福建省科委優秀論文一等獎。在數學的其他...
