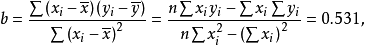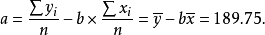一元線性回歸方程的形式
如果只有一個自變數X,而且因變數Y和自變數X之間的數量變化關係呈近似線性關係,就可以建立一元線性回歸方程,由自變數X的值來預測因變數Y的值,這就是一元線性回歸預測。
如果因變數Y和自變數X之間呈線性相關,那就是說,對於自變數X的某一值
,因變數Y對應的取值
不是唯一確定的,而是有很多的可能取值,它們分布在一條直線的上下,這是因為Y還受除自變數以外的其他因素的影響。這些因素的影響大小和方向都是不確定的,通常用一個隨機變數(記為
)來表示,也稱為
隨機擾動項。於是,Y和X之間的依存關係可表示為
式(1)就是總體的
一元線性回歸模型。其中
是常數。隨機擾動項
是無法直接觀測的隨機變數。為了進行回歸分析,通常假定
,即假定
是零均值
、同方差
、相互獨立
且服從常態分配的。
對式(1)求均值則有:
通常將式(2)稱為總體的
一元線性回歸方程或
總體回歸直線,以
表示給定自變數值
時因變數的均值或期望值。
統稱為總體回歸方程的參數。其中
是
總體回歸方程的常數項,是總體回歸直線在Y軸上的截距;
是
總體回歸係數,也是總體回歸直線的斜率。由式(2)不難理解,總體回歸方程描述的是Y和X兩個變數之間平均的數量變化關係。
在實際中,通常由於不可能把變數的全部可能取值收集齊全,總體回歸方程中的參數
是不可能直接觀測計算而得的,是有待估計的未知參數。為此,我們需要根據樣本信息來估計。若能通過適當的方法,找到兩個樣本統計量a、b分別作為參數
的估計量,那么用a、b分別替代總體回歸方程中的參數
,則得到估計的回歸方程,也稱
樣本回歸方程。一元線性的樣本回歸方程也稱為
樣本回歸直線,其形式如下:
式中,
是與自變數取值
相對應的因變數均值
的估計;a和b分別為總體回歸方程參數
的估計量,a是樣本回歸方程的常數項,也就是樣本回歸直線在Y軸上的截距,表示除自變數X以外的其他因素對因變數Y的平均影響量;b是樣本回歸係數,也即樣本回歸直線的斜率,表示自變數X每增加一個單位時因變數Y的平均增加量。
根據樣本觀察數據估計出a和b的數值之後,樣本回歸方程(3)可作為預測模型,即一元線性回歸預測模型。
一元線性回歸方程參數的估計
最小平方法
如何確定式(3)中的兩個係數a和b呢?人們總是希望尋求一定的規則和方法,使得所估計的樣本回歸方程是總體回歸方程的最理想的代表。最理想的回歸直線應該儘可能從整體來看最接近各實際觀察點,即
散點圖中各點到回歸直線的垂直距離,即因變數的實際值
與相應的回歸估計值
的離差整體來說為最小。由於離差有正有負,正負會相互抵消,通常採用觀測值與對應估計值之間的
離差平方總和來衡量全部數據總的離差大小。因此,回歸直線應滿足的條件是:全部觀測值與對應的回歸估計值的
離差平方的總和為最小,即:
根據式(4)的準則來估計回歸方程係數a和b的方法稱為
最小平方法或
最小二乘法。顯然,在給定了X和Y的樣本觀察值之後,離差平方總和的大小依賴於a和b的取值,客觀上總有一對a和b的數值能夠使離差平方總和達到最小。利用
微分法求函式極值的原理,即可得到滿足式(4)的兩個正規方程:
解上述方程可以求得a和b。通常將a和b的計算公式寫為如下形式:
套用實例
【例1】為了研究某地區某行業企業廣告支出對銷售收入的影響,隨機抽取了8個企業,調查得知它們的廣告費與銷售額的數據如表1的第(1)和(2)列所示,試建立企業廣告費與銷售額之間的回歸方程。
序號 | 廣告費x(萬元) | 銷售額y(百萬元) | xy | x2 | y2 |
(甲) | (1) | (2) | (3) | (4) | (5) |
1 | 300 | 300 | 90000 | 90000 | 90000 |
2 | 400 | 350 | 140 000 | 160 000 | 122 500 |
3 | 400 | 490 | 196 000 | 160 000 | 240 100 |
4 | 550 | 500 | 275 000 | 302 500 | 250 000 |
5 | 720 | 600 | 432 000 | 518400 | 360000 |
6 | 850 | 610 | 518 500 | 722 500 | 372 100 |
7 | 900 | 700 | 630000 | 810 000 | 490000 |
8 | 950 | 660 | 627 000 | 902 500 | 435 600 |
合計 | 5 070 | 4 210 | 2 908 500 | 3 665 900 | 2 360 300 |
解:通常企業的廣告投入越多,產品銷售額就會越多,但是具有相同廣告支出的企業,其產品銷售額並不完全相同,因為企業銷售額不僅受廣告投入的影響,同時還受許多其他因素的影響,這些影響因素存在不確定性,甚至有些是無法觀察的。所以,企業的廣告費與產品銷售額之間的關係不是
函式關係而是
相關關係。廣告費支出顯然是影響銷售額的一個重要因素,應該以廣告費為自變數X,以銷售額為因變數Y。觀察廣告費與銷售額的相關關係的形態需繪製
散點圖(
相關圖)。在Excel中,先將X、Y兩個變數的數據放在相鄰兩列或兩行(X在前,Y在後),然後用滑鼠選定數據區域,再單擊選單欄“插入”下的“圖表”,選擇標準類型中的“XY散點圖”即可(也可先選定“XY散點圖”後在空白圖形中單擊右鍵“選擇數據”再指定X和Y的數據所在區域)。在SPSS中,單擊選單欄的“圖形(Graphs)”,選擇其下的“散點圖/點圖(Scatter)”,在隨即彈出的子圖形類型中選擇第一個圖形,即
簡單散點圖,將所分析的變數分別選入Y軸和X軸即可。
由表1的第(1)和(2)列的數據繪製相關圖,如圖1所示。
 圖1 廣告費與銷售額的相關圖
圖1 廣告費與銷售額的相關圖由圖1可知,隨著廣告費的增加,企業銷售額也相應增加,而且樣本點的分布僅僅圍繞在一條直線上下,表明銷售額Y與廣告費X之間存在非常密切的線性正相關關係,所以銷售額Y與廣告費X的回歸方程應該是個一元線性回歸方程。圖中的直線正是所要求的樣本回歸直線,其對應的數學表達式就是我們所要估計的一元線性回歸方程。先列表計算出估計一元線性回歸方程參數所需數據,如表1的第(3)至(4)列所示。由式(6)可計算回歸方程參數的估計值為
上述回方程表明,如果沒有廣告投入(x=0 時),銷售額平均只有189.75百萬元。
廣告費每增加1萬元,企業銷售額將平均增加53.1萬元。
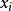





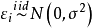

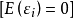

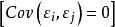
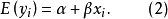
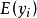

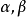
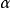

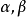
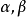
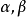



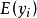
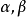


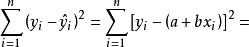
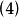


 圖1 廣告費與銷售額的相關圖
圖1 廣告費與銷售額的相關圖