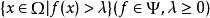α細拓撲

α細拓撲是使每個α上調和函式都連續的最粗拓撲。α細拓撲比歐氏拓撲細且當α<α'時，α細拓撲嚴格細於α細拓撲。

基本介紹

• 中文名：α細拓撲
• 外文名：α-fine topology
• 適用範圍：數理科學

簡介

α細拓撲是使每個α上調和函式都連續的最粗拓撲。

在Rⁿ上，取Φ為非負α上調和函式(0<α≤2,α<n)全體及+∞時所得的T稱為a細拓撲。

性質

α細拓撲比歐氏拓撲細且當α<α'時，α細拓撲嚴格細於α細拓撲。

α細拓撲下的開集、閉集、極限、瘦等概念分別稱為α細開集、α細閉集、α細極限、α瘦等。

細拓撲

(fine topology)

細拓撲是由給定的下半連續函式族確定的、比原來拓撲細的一種拓撲。

在非空集合Ω上賦予拓撲T，設Φ是一族從(Ω，T)到[0，+∞]的下半連續函式組成的凸錐(設+∞∈Φ)，把形如：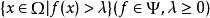

的集全體記為S，那么S∪T所生成的拓撲T₀是使Φ中每個函式都連續的最粗拓撲，稱之為（相對於Φ與T的）細拓撲。

細拓撲下的開集、閉集、閉包、極限等分別稱為細開集、細閉集、細閉包、細極限等。在格林空間中，若不另作申明，則總認定Φ是非負超調和函式全體。一般地，談及細與瘦的概念時，都假定有了確定的Φ與T。