m/m/1

M/M/1排隊模型（M/M/1 model）是一種單一伺服器（single-server）的（排隊模型），可用作模擬不少系統的運作。

定義

依據開恩特羅符號必須有下列的條件：

到達人數是泊松過程（Poisson process）；

服務時間是指數分布（exponentially distributed）；

只有一部伺服器（server）

佇列長度無限制

可加入佇列的人數為無限

分析

這種模型是一種出生-死亡過程，此隨機過程中的每一個狀態代表模型中人數的數目。因為模型的佇列長度無限且參與人數亦無限，故此狀態數目亦為無限。例如狀態0表示模型閒置、狀態1表示模型有一人在接受服務、狀態2表示模型有二人（一人正接受服務、一人在等候），如此類推。 此模型中，出生率（即加入佇列的速率）λ在各狀態中均相同，死亡率（即完成服務離開佇列的速率）μ亦在各狀態中相同（除了狀態0，因其不可能有人離開佇列）。故此，在任何狀態下，只有兩種事情可能發生：

有人加入佇列。如果模型在狀態k，它會以速率λ進入狀態k + 1

有人離開佇列。如果模型在狀態k（k不等於0），它會以速率μ進入狀態k − 1

由此可見，模型的隱定條件為λ < μ。如果死亡率小於出生率，則佇列中的平均人數為無限大，故此這種系統沒有平衡點。

佇列參數表示

• λ：平均到達的顧客數（單位時間平均到達率，個/秒）
  
• μ：平均服務的顧客數（服務率、離開率,個/秒），每客平均服務時間 T= 1/μ,
  
• Lq:平均等待佇列長度（在佇列中排隊等待的顧客數）
  
• Wq:每個顧客的平均等待時間，包括沒有排隊的顧客
  
• L：系統中平均顧客數=正在被服務的顧客數+正在等待的顧客數
  
• W：平均等待時間=平均等待時間+平均服務時間
  
• ρ:平均利用率，一段相當長的時間內可測得 = λ/μ≤1
  

公式

定義

則模型在狀態i的機率為

由此，可給出各測量數值的公式：

整個系統的平均人數N：

，且其變異（variance）為：（方差）

一單位時間內系統完成服務的人數：

在佇列中等候服務的人數：

一人在系統中的平均逗留（等候+接受服務）時間：

一人的平均等候時間：

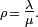
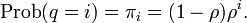
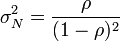
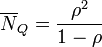
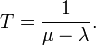
問題

求系統在任意時刻t的狀態n

系統中有n個顧客的機率Pn(t),它決定了系統運行的特徵。
穩定情況下，Pn(t)與t無關，Pn(t)=Pn;
狀態轉移平衡方程：轉入率=轉出率；
狀態i轉移到狀態i+1的轉移率λiPi;
狀態i+1轉移到狀態i的轉移率μi+1Pi+1;
狀態平衡方程：Rate In = Rate Out
0 u1P1= λ0P0
1 λ0P0+ u2P2= (λ1+ u1) P1
2 λ1P1+ u3P3= (λ2+ u2) P2

.... ....................... ...................
N -1 λN -2PN -2+ uNPN= (λN -1+ uN -1) PN -1
N λN -1PN -1+ uN+1PN+1= (λN+ uN) PN
.... ...................

求穩態狀態解:

狀態：0: P1= (λ0 / u1) P0
狀態：1: P2= (λ1 / u2) P1+ (u1P1- λ0P0) / u2
= (λ1 / u2) P1+ (u1P1- u1P1) / u2
= (λ1 / u2) P1
=(λ1λ0/u2u1)P0
狀態：n-1: Pn= (λn -1 / un) Pn -1+ (un -1Pn -1- λn -2Pn -2) / un
= (λn -1 / un) Pn -1+ (un -1Pn -1- un -1Pn -1) / un
= (λn -1 / un) Pn -1
=(λn-1λn-2λn-3....λn0/un-1un-2un-3...u1)P0
狀態：n : Pn+1= (λn / un+1) Pn+ (unPn - λn -1Pn -1) / un+1
= (λn / un+1) Pn
=(λnλn-1λn-2λn-3....λn0/unun-1un-2un-3...u1)P0

簡化過程:

Let C = (λn-1λn-2λn-3....λn0/un-1un-2un-3...u1)
then Pn = CnP0,Cn = （λ/u）^n = P^n
又∑Pi = 1，則 P0 = 1-ρ
Pn = CnP0 = (1-ρ)ρ^n

M/M/1 系統的隊長

用 表示正在排隊的顧客長度（不包括正在接受服務的顧客）， 表示系統的排隊長度（包括正在接受服務的顧客），則：

或者，將 替換為 得到

舉例

可用M/M/1模型的例子眾多，例如只有一位員工的郵局，只有一佇列。客人進來，排隊、接受服務、離開。如果客人進來的數目符合泊松過程，且服務時間是指數分布，則可用M/M/1模擬，並算出平均佇列長度、不同等候時間的機率等。

M/M/1可一般化成為M/M/n模型，使可用時接受服務的人數為大於一。歷史上，M/M/n模型首先被用來模擬電話系統，因為荷蘭工程師Erlang發現客人打電話的速率符合泊松過程，且通話時間是指數分布，所以占用通訊線路的數目和等待接線的人數符合M/M/n模型。