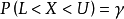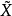z分數（z-score），也叫標準分數（standard score）是一個數與平均數的差再除以標準差的過程。在統計學中，標準分數是一個觀測或數據點的值高於被觀測值或測量值的平均值的標準偏差的符號數。
z分數可以回答這樣一個問題："一個給定分數距離平均數多少個標準差?"在平均數之上的分數會得到一個正的標準分數，在平均數之下的分數會得到一個負的標準分數。 z分數是一種可以看出某分數在分布中相對位置的方法。
基本介紹
- 中文名：Z分數
- 外文名：z-score
- 中文別名：標準分數，標準化變數
- 英文別名：standard score
- 類別：數學術語
- 屬於：統計學
定義,公式,套用,標準化,T分數,
定義
z分數能夠真實的反應一個分數距離平均數的相對標準距離。如果我們把每一個分數都轉換成z分數，那么每一個z分數會以標準差為單位表示一個具體分數到平均數的距離或離差。將成常態分配的數據中的原始分數轉換為z分數，我們就可以通過查閱z分數在正態曲線下面積的表格來得知平均數與z分數之間的面積，進而得知原始分數在數據集合中的百分等級。一個數列的各z分數的平方和等於該數列數據的個數，並且z分數的標準差和方差都為1.平均數為0.
公式
總體z分數：
。其中μ為總體平均值，X-μ為離均差，σ表示總體標準偏差。z的絕對值表示在標準差範圍內的原始分數與總體均值之間的距離。當原始分數低於平均值時，z為負，以上為正。
其中，計算z需要總體平均數和總體標準偏差，而不是樣本平均值或樣本偏差。 它需要知道總體參數，而不是從感興趣的總體中抽取樣本的統計數據。但可以使用隨機樣本來估計標準偏差。
z分數測量實際數據的平均距離。
z值提供了對偏離目標的評估。
樣本z分數：
套用
z分數常用於標準化考試的z - test——模擬學生的t檢驗，而不是估計其參數。由於了解整個總體的情況很複雜，所以t檢驗被廣泛套用。
此外，標準分數可用於計算預測區間。一個預測區間[L,U]，由一個較低的端點指定的L和一個上端點指定的U組成，這是一個區間，未來的觀察值X將在高機率γ伽瑪的區間內，即
對於標準分數Z(X)，給出：
。
通過確定z分數，
它遵循：
標準化
在數學統計中，任意變數X的標準化過程是減去它的期望值E(X)並且除以它的標準差
，即：
T分數
在教育評估中，T分數是一個標準分數Z，並且平均數為50，標準偏差為10。
在骨密度測量中，與健康30歲成年人的人群相比，T評分是測量的標準評分。
