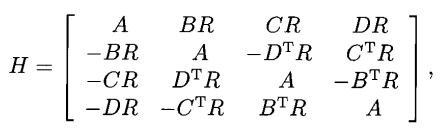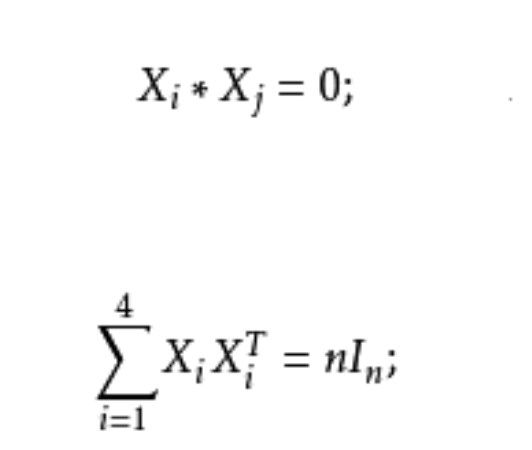T矩陣

T矩陣(T-matrix)是一類特殊的矩陣，可用於構作鮑默特-霍爾表，若G={g₁，g₂，…，g_n}為加法可換群，X⊆G，M=(m_ij)，當g_j-g_i∈X時m_ij=1，否則m_ij=0，則稱M是關於X的Ⅰ型關聯矩陣，若X可劃分為X=X₁∪X₂，使g_j-g_i∈X₁時m_ij=1，g_i-g_j∈X₂時m_ij=-1，g_j-g_i∉X時m_ij=0，則稱M為Ⅰ型(0，1，-1)矩陣，若M₁，M₂，M₃，M₄是n階可換群G上的4個(0，1，-1)矩陣，使對n個位置的每一個恰有一個M_i在此位置上元素不為零，且M₁M₁+M₂M₂+M₃M₃+M₄M₄=nI_n，其中I_n為單位矩陣，則稱這4個矩陣為T矩陣，若存在t階T矩陣，則存在t階鮑默特-霍爾表BH[4t]，許多已知的BH[4t]是從T矩陣得到的。

基本介紹

• 中文名：T矩陣
• 外文名：T-matrix
• 所屬學科：數學
• 所屬問題：組合數學（組合設計理論）
• 簡介：一類特殊的矩陣

基本介紹

設

是長為n的(0,±1)-序列，若

(i)對1≤j≤n，恰有一個為±1,其餘3個均為0，

(ii)對1≤j≤n-1,恆有

則稱是一組不相交T-序列。簡稱T-序列(T-sequence)。

對上述T-序列，設1≤i≤4，令X_i表示以A_i為第一行而生成的n階循環矩陣，則稱為一組n階不相交循環T-矩陣，簡稱循環T-矩陣。

用T-矩陣構造Baumert-Hall陣列

引理1設為n階循環T-矩陣。則

(i)1≤i,j≤4,i≠j,則X_i與X_j不相交,即

(ii)是一個(1,-1)-矩陣；

(iii)

(iv)對1≤i≤4,X_i的各行和都相等,設X_i的行和為n_i,則

下述定理給出構作Baumert-Hall陣列的一個強有力方法。

定理1(Cooper，J.Wallis) 設為n階循環T-矩陣，a，b，c，d為交換變元，令

再設R為下述n×n矩陣：

式（7）

將式(6)與式(7)代入下述Goethal-Seidel陣列

式（8）

則得到一個OD(4n；n，n，n，n)。

在上述定理中，若取a=b=c=d=1，則得到一個4n階H-陣，於是得到下述結果。

定理2若存在一組長為n的T-序列。則存在4n階H-陣。

由定理1與定理2可見T-序列在構作Baumert-Hall陣列和Hadamard矩陣時所起的重要作用。一般來說，尋求長為n的T-序列並不容易。由引理1之(iv)可知。設是一組長為n的T-序列，又設A_i中所有元素的和為n_i，1≤i≤4，則必有

這一觀察有助於尋找T-序列。由Lagrange四平方和定理，任一正整數n都能表為4個非負整數的平方和，但是否對每一個正整數n都存在長為n的T-序列?這是一個尚未解決的問題，從對構作Hadamard矩陣的套用而言，我們主要關心n為奇數時T-序列的存在性。

猜想1 設n≥1為奇數，則存在長為n的T-序列。

若上述猜想成立，則作為其推論，Hadamard猜想也就得到證明。

定理3若4n≤200，則4n階H-陣存在。