基本介紹
- 中文名:radon變換
- 外文名:Radon transform
- 對應:原始函式的某個線積分值
- 含有:直線成分
- 按照:合適的角度
簡介
定義
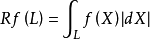

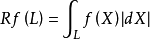
數學上,是一種積分變換,這個變換將二維平面函式F變換成一個定義在二維空間上的一個線性函式RF(RF的意思是對F 做radon變換),而RF 的值為函式F對該條線RF做...
τ-p變換(又稱傾斜疊加)是離散化的Radon變換。其基本原理是:對於時空域x-t域的一個共炮點(CSP)道集地震記錄Φ(x,t)利用如下τ-p正變換(傾斜疊加)便可...
7.2 小波RADON變換檢測線性調頻信號參數 2477.2.1 線性調頻信號的小波分析結果的時間尺度和時頻表示 2487.2.2 通過RADON變換檢測時頻平面上的直線 250...
《快速傅立葉變換:算法與套用》是2013年出版的一本圖書,作者是K.R.Rao。...... 8?30快速均勻離散曲波(curvelet)變換(FUDCuT)2618?30?1Radon變換262...
通過時頻分布檢測線性調頻信號比較直觀, 線性調頻信號在時頻平面上呈現為直線形狀 ,通過 Radon 變換檢測時頻平面上的直線, 可以得到調頻信號參數。通過雙線性變換的...
第5章:圖像變換技術。主要介紹了正交變換通用運算元、傅立葉變換、離散餘弦變換、Radon變換等內容。 第6章:圖像的增強處理。主要介紹了灰度變換增強、空域濾波增強、頻...
實驗二離散餘弦變換練習實驗三小波變換練習實驗四Radon變換練習第5章形態學圖像處理5.1數學形態學的集合論基礎5.2二值形態學5.3灰度形態學...
1.4.1基於經典傅氏變換的去噪方法l.4.2在傅氏變換基礎上延伸出來的去噪方法1.4.3以Radon變換為基礎的去噪方法1.4.4聚束濾波方法...
5.3.3一維離散哈達瑪變換5.3.4二維離散哈達瑪變換5.3.5離散沃爾什-哈達瑪變換的套用舉例5.4K-L變換5.4.1K-L變換的定義5.4.2K-L變換的性質5.5Radon變換...
4.1.4傅立葉變換的實現4.1.5傅立葉變換的套用4.2離散餘弦變換4.3離散哈達瑪變換4.4Radon變換4.4.1Radon變換的定義4.4.2Radon變換檢測直線...
例7-8 Radon變換。 133例7-9 使用Radon變換來檢測直線。 133例7-10 逆Radon變換重建圖像。 135第8章 圖像的增強 136例8-1 直方圖的顯示。 136...
3.3 Radon變換3.3.1 Radon變換基礎知識3.3.2 Radon變換的MATLAB函式3.3.3 實例操作3.4 Fan-Beam變換3.4.1 Fan-Beam變換基礎知識...
第4章 數字圖像的變換域處理 4.1 傅立葉變換 4.2 離散餘弦變換 4.3 離散哈特利變換 4.4 方波型變換 4.5 基於特徵分析的變換 4.6 小波變換 4.7 Radon變換 4.8 ...
