基本介紹
- 中文名:PID算法
- 外文名:Proportion Integral Differential
- 最初套用:船舶自動舵
- 最初套用時間:19世紀70年代
- 套用範圍:工業控制,船舶自動舵等
簡介
PID控制原理和算法
PID作用
 圖1
圖1 圖2
圖2 圖3
圖3 圖4
圖4PID參數調節
算法種類
PID增量式算法
PID位置算法

遇限削弱積分法
積分分離法




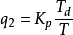

 圖1
圖1 圖2
圖2 圖3
圖3 圖4
圖4




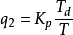
在過程控制中,按偏差的比例(P)、積分(I)和微分(D)進行控制的PID控制器(亦稱PID調節器)是套用最為廣泛的一種自動控制器。它具有原理簡單,易於實現,適用面廣,...
PID=port ID,在STP(生成樹協定)中,若在連線埠收到的BPDU中BID和path cost相同時,則比較PID來選擇阻塞連線埠。數位電視復用系統名詞 PID(Packet Identifier) 在數字...
自從計算機和各類微控制器晶片進入控制領域以來,用計算機或微控制器晶片取代模擬 PID控制電路組成控制系統,不僅可以用軟體實現 PID 控制算法,而且可以利用計算機和微...
增量式PID控制,數字PID控制算法的一種基本形式,是通過對控制量的增量(本次控制量和上次控制量的差值)進行PID控制的一種控制算法。...
PID控制器產品,各大公司均開發了具有PID參數自整定功能的智慧型調節器(intelligent regulator),其中PID控制器參數的自動調整是通過智慧型化調整或自校正、自適應算法來...
PID整定即PID參數整定。PID控制器中,需對P、I、D三個參數進行設定,一般通過工程人員的經驗技巧進行湊試,此過程即為PID整定,目前對PID參數自動整定已有大量研究...
PID參數整定是一個複雜的過程,一般需要根據被對象慢慢進行。常用的方進有擴充臨界比例度整定法和擴充回響曲線法兩種。適合計算機控制用的簡易方法一簡化擴充臨界比例...
PID控制器(比例-積分-微分控制器),由比例單元(P)、積分單元(I)和微分單元(D)組成。透過Kp,Ki和Kd三個參數的設定。PID控制器主要適用於基本上線性,且動態特性...
PID控制是一個在工業控制套用中最為廣泛的控制算法,由於各種原因,會造成PID控制器性能下降,體現在工藝上,會造成工藝波動,進而影響生產效率。為了更好地發揮PID控制...
PID算法與模糊控制理論相結合的一種控制理論。...... PID算法與模糊控制理論相結合的一種控制理論。中文名 模糊PID 外文名 Fuzzy PID 套用 工業控制等 目錄 1...
在工業過程控制中,按被控對象的實時數據採集的信息與給定值比較產生的誤差的比例、積分和微分進行控制的控制系統,簡稱PID控制系統。PID控制具有原理簡單,魯棒性強和...
PID控制器產品,各大公司均開發了具有PID參數自整定功能的智慧型調節器(intelligent regulator),其中PID控制器參數的自動調整是通過智慧型化調整或自校正、自適應算法來...
非線性PID控制是利用非線性特性對PID控制的一種改進,從而提高控制器的魯棒性和適應性。它利用非線性結構的跟蹤-微分器產生控制器所需的比例、積分和微分信號,並...
PID控制模組是許多控制策略的關鍵,它幾乎被普遍使用,除PD之外,當過程本身有偏差存在時,PID模組輸出將不斷變化,輸出使偏差向減小方向變化(這是對負反饋控制系統而言...
變參數 PID 控制,簡稱VAPID,它是根據誤差信號 e 的變化對 PID 控制器各參數進行線上整定 。利用變參數PID 控制則可以很好地解決常規控制器對工況的適應性問題。...
自適應PID控制,是指自適應控制思想與常規PID控制器相結合形成的自適應PID控制或自校正PID控制技術,人們統稱為自適應PID控制。...
《可程式序控制器模擬量及PID算法套用案例》是由霍罡編寫,高等教育出版社出版的一本書籍。...
在普通PID控制中引入積分的目的,主要是為了消除靜態誤差,提高控制精度。但在過程的啟動、結束或大幅度增減設定值時,短時間內系統輸出很大的偏差,會造成PID運算的積分...
本書在介紹數字PID控制的基礎上,分別闡述了自適應PID控制、智慧型PID控制、模糊PID控制、神經網路PID控制、預測PID控制和PID控制器自整定技術。在介紹這些控制時都附...
《PID神經元網路及其控制系統》是 2006年國防工業出版社 出版的圖書,作者是 舒懷林 。...
《PID控制器參數整定與實現》是由黃友銳,曲立國編寫,科學出版社出版的一本書籍。...... 數字PID控制器的FPGA實現;基於BP神經網路的PID控制器的FPGA實現;基於遺傳...
《先進PID控制MATLAB仿真》是2011年電子工業出版社出版的圖書,作者是劉金琨。...... PID控制、神經PID控制、基於遺傳算法整定的PID控制、伺服系統PID控制、疊代學習PID...
pid調節控制儀是一種的智慧型數顯調節儀表。它採用專家pid控制算法,控制精確穩定,無超調,無欠調現象,能用於溫度、壓力、液位、流量的定值控制,適用於熱電阻、熱電...
概括地講,PID 控制的優點主要體現在:原理簡單、實現方便,是一種能夠滿足大多數實際需要的基本控制器。控制器適用於多種截然不同的對象,算法在結構上具有較強的...
模糊自適應PID控制是在PID算法的基礎上,以誤差e和誤差變化率ec作為輸入,利用模糊規則進行模糊推理,查詢模糊矩陣表進行參數調整,來滿足不同時刻的e和ec對PID參數自...
