藥物在體內的降解速率在數學上呈非線性關係的速率過程。
用於描述藥物代謝動力學的一種速率過程。
用米-曼方程描述。
基本介紹
- 中文名：米-曼速率過程
- 外文名：Michaelis-Menten
- 別名：非線性動力學過程
概念,描述方程,套用,其他套用場合,例子,
概念
某些藥物在體內的降解速率受酶活力的限制，通常在高濃度時是零級速率過程，而在低濃度時是一級速率過程，稱Michaelis-Menten速率過程。
描述方程
Michaelis-Menten方程：
Vm表示該過程最大速率，Km是Michaelis常數，指變化速率為最大速率一半時的藥物濃度。
（1）當藥物濃度很大時，即C>>Km：
此時服從零級動力學，其積分式為：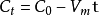
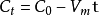
藥物半衰期為：
(2)當藥物濃度很小時，即C<<K，令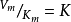
，則服從一級速率過程
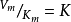
套用
其他套用場合
某些藥物是以主動轉運方式進行的，當藥物達到一定濃度後，其載體飽和，此時轉運速率達到恆定值，再增加藥量，轉運速率不變，這類藥物的動力學通常也以Michaelis-Menten動力學過程來描述。
例子
苯妥英鈉（phenytoin sodium）
高劑量的巴比妥類
硫噴妥鈉（thiopental sodium）
地高辛（digoxin）
水楊酸鹽（salicylate）
雙香豆素（dicoumarol）
