基本介紹
調節裝置介紹,裝置設計優勢,
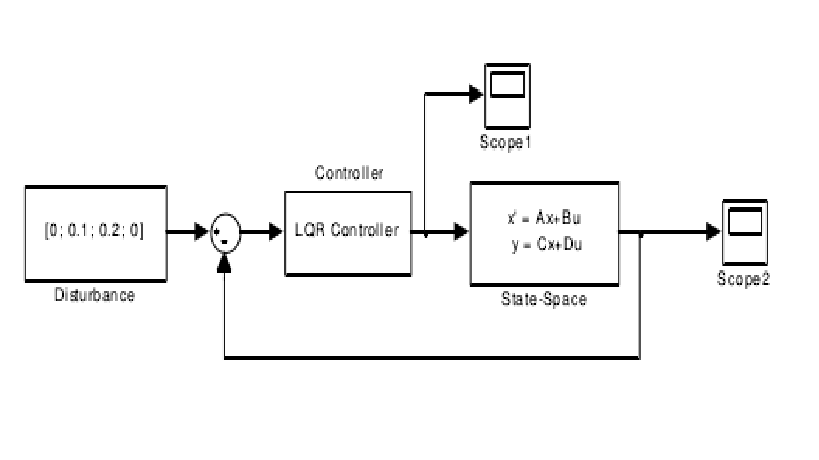
LQR (外文名linear quadratic regulator)即線性二次型調節器,LQR可得到狀態線性反饋的最優控制規律,易於構成閉環最優控制。LQR最優控制利用廉價成本可以使原系統達到...
4.3.2LQR控制算法 4.3.3環形二級倒立擺的LQR控制器設計及驗證 第五章DCS控制系統設計 5.1DCS的體系結構 5.2幾種典型的DCS簡介 5.3HOLLiASMACS在催化...
線性二次型調節器( Linear Quadratic Regulator,LQR) 控制由於反饋增益可以採用誤差狀態的線性反饋控制律構成最優閉環,設計時能夠考慮允許的狀態偏差和控制量偏差等多...
4.8.3固定增益LQR設計 4.8.4CMAPSS—40k中的固定增益LQR 4.8.5H2/H∞固定增益綜合:多胞對象模型 4.9簡化的H∞風扇轉速控制 4.9.1混合靈敏度H∞設計 ...
