Klein-Nishina公式

Klein-Nishina公式是用以計算電磁場對靜止電子的康普頓散射微分散射截面與初、末態光子能量的公式。1929年最早由O.Klein和Y.Nishina得到。

基本介紹

• 中文名：Klein-Nishina公式
• 外文名：Klein-Nishina formula
• 提出者：O.Klein, Y.Nishina
• 提出時間：1929年
• 適用領域：量子場論
• 套用學科：物理學

定律定義

Klein-Nishina公式是用以計算電磁場對靜止電子的康普頓散射微分散射截面與初、末態光子能量的公式。

其用於計算圖1過程的微分散射截面：

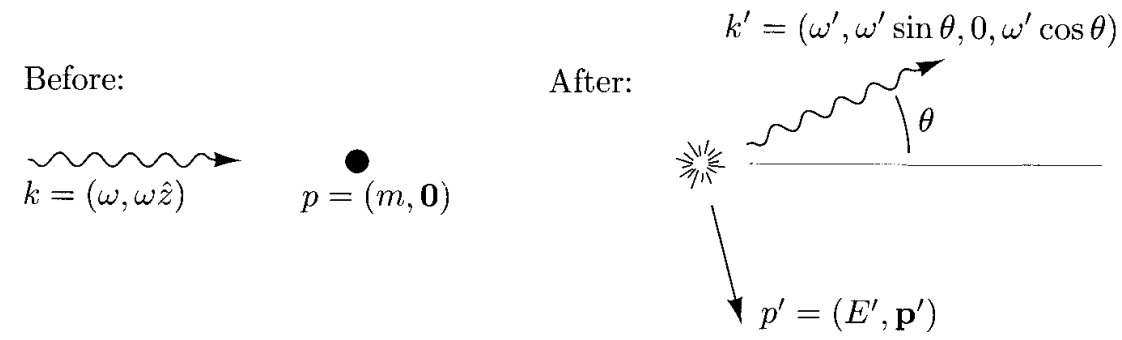
圖1

公式的表達式為：

其中：

推導過程

具體計算康普頓散射的樹圖結果可以得到Klein-Nishina公式，具體來說就是要計算圖2中的兩個圖：

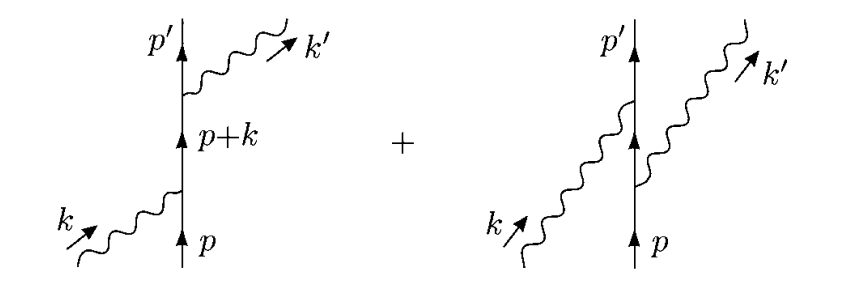
圖2

其費曼散射振幅可以表達為：

對費曼振幅平方後極化求和、求平均後可得：

代入圖1中定義的四動量，再利用：

其中A、B為初態粒子，f為末態粒子，對相空間積分就可得到：

發展簡史

Klein-Nishina公式是對自旋求平均得到的結果，該結果1929年最早由O.Klein和Y.Nishina得到。

套用領域

在電子與高能光子發生康普頓散射的實驗領域，Klein-Nishina公式具有良好的預言性。

定律影響

康普頓散射實驗可以很好的驗證光的波粒二象性，此外Klein-Nishina公式的成功也客觀得驗證了量子場論這套方法的可行性，此外也給QED（量子電動力學）以很好的實驗佐證。