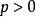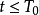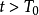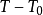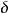KMRW聲譽模型

KMRW聲譽模型，又稱“四人幫”模型。克瑞普斯、米爾格羅姆、羅伯茨和威爾遜（Kreps，Milgrom，Roberts and Wilson，1982）的KMRW聲譽模型證明，參與人對其他參與人支付函式或戰略空間的不完全信息對均衡結果有重要影響，合作行為在有限次重複博弈中會出現，只要博弈重複次數足夠長。

基本介紹

• 中文名：KMRW聲譽模型
• 外文名：KMRW reputation model
• 又稱：四人幫”模型
• 隸屬：數理科學
• 學科：運籌學
• 歸屬：聲譽模型

相關概念

在完全信息情況下，不論博弈重複多少次，只要重複的次數是有限的，唯一的子博弈精煉納什均衡是每個參與人在每次博弈中選擇靜態均衡戰略(假定靜態博弈的納什均衡是唯一的)，即有限次重複不可能導致參與人的合作行為。特別地，在有限次重複囚徒博弈中，每次都選擇“坦白”是每個囚徒的最優戰略。 這一結果似乎與人們的直觀感覺不一致。阿克賽爾羅德(Axelrod，1981和1984年)的錦標賽實驗結果表明，在200次有限次重複囚徒博弈中，合作行為頻繁出現，而“針鋒相對”戰略是最穩健的戰略。

“理什囚徒”只是對我們已經熟悉的“囚徒”及其行為的一個簡單化概括，這裡可以理解為機會主義者，或者非合作型參與人； “非理性囚徒”是對具有不同於我們熟悉的行為方式的另一類囚徒的概括，這裡可以理解為講義氣重信譽的人，或者合作型參與人。

基本內容

在T階段重複囚徒博弈中，如果每個囚徒都有 的機率是非理性的(即只選擇“針鋒相對”或“冷酷戰略”)，如果T足夠大，n那么存在一個 ，使得下列戰略組合構成一個精煉貝葉斯均衡：

所有理性囚徒在 階段選擇合作(抵賴)，在 階段選擇不合作(坦白)；並且，非合作階段的數量 只與p有關，而與T無關。

直觀解釋

1. 儘管每一個囚徒在選擇合作時冒著被其他囚徒出賣的風險(從而可能得到一個較低的現階段支付)，但如果他選擇不合作，就暴露了自己是非合作型的，從而失去了獲得長期合作收益的可能，如果對方是合作型的話；
   
2. 如果博弈重複的次數足夠多，未來收益的損失就超過了短期被出賣的損失，因此，在博弈的開始，每一個參與人都想樹立一個合作形象(使對方認為自己是喜歡合作的)，即使他在本性上並不是合作型的；
   
3. 只有在博弈快結束的時候，參與人才會一次性地把自己的過去建立的聲譽利用盡，合作才會停止，因為此時，短其收益很大而未來損失很小；
   
4. KMRW定理解釋了“大智若愚”，這裡，智者囚徒博弈中的理性囚徒(非合作型)，“愚者”即囚徒博弈中的非理性囚徒(合作型)。 在許多情況下，大智若愚確實是“智者”追求自己利益的最佳方式。
   

意義

只要博弈重複的次數足夠長，參與人有足夠的耐心(只要足夠接近於1)，即使(有關參與人類型的)小小的不確定性，也可能引起均衡結果的重大改變（很小的p就可以保證合作均衡的出現，但如果p=0，合作均衡不可能出現）。 當然，合作均衡的可能性依賴於我們有關非理性參與人行為的假定。比如，如果我們假定，不論對方選擇什麼，非理性囚徒總是選擇D(合作)，那么，合作均衡就不會出現，因為，給定非理性囚徒總是選擇D的情況下，C是理性囚徒的占優戰略。如果不論你如何損害對方的利益，對方總是“以德報怨”、"仇將恩報"。

KWRW模型解開了有限重複博弈的悖論，但也帶來了均衡的多重性問題。 弗登伯格和馬司肯（1986年）證明，類似完全信息無限重複博弈的“無名氏定理”在不完全信息有限重複博弈中也成立，只要博弈重複的次數足夠長，參與人有足夠的耐心，任何滿足個人理性的可行支付向量，都可以作為精煉貝葉斯均衡結果出現，不論p多么小。