GB系統概括原則

GB系統概括原則(comprehension principle of GB system) GB系統的一個元定理。

對於GB系統的任一直謂公式}p<xxz,...}x}}'i,Yz,...}y,.,)，存在一個類A(它當然依賴於Yi,Yz,...,y,)使得

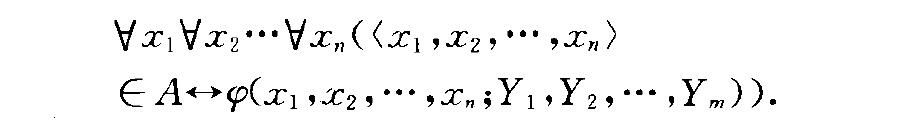
公式

其中小寫字母是集合變元，大寫字母是類變元.此定理保留了康托爾集合論中概括原則的主要精神:一個謂詞決定一個類.但有兩處修改，一是謂詞必須由直謂公式表示;二是構成的類不一定是集合，即不一定能出現在任號之前.正是作了這樣的修改，才得以避免羅素悖論的出現.

王浩(Wang, H.)指出，若去掉對合式公式的 “直謂”要求，即允許公式抓x} ,xz, ".. },x})中出現約束真類變元，則命題模式

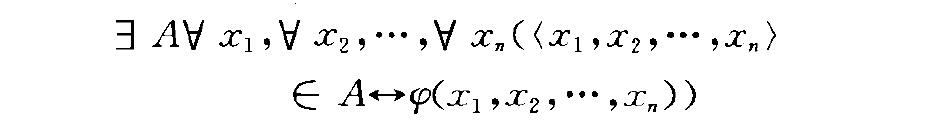
公式

不可化歸為有限條公理，而且，該命題與GB系統是相對相容的.