基本介紹
- 中文名:Contourlet變換
- 屬性:圖像原理
- 時間:2002年
- 提出者:Do和Vetterli
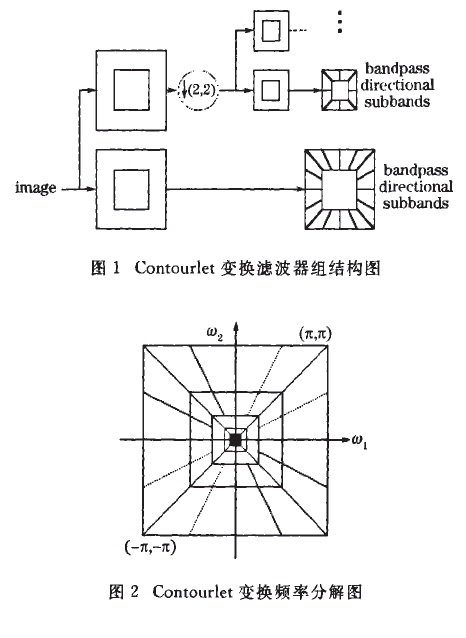
2002年Do和Vetterli在繼承小波多尺度分析思想的基礎上提出一種新的非自適應的方向多尺度分析方法——Contourlet變換,它能在任意尺度上實現任意方向的分解,擅長描述圖像...
《Contourlet變換:影像處理套用》是2008年由科學出版社出版的圖書。本書以Contourlet變化在圖像處理中的套用為研究對象,介紹了Contourlet變換在影像壓縮、超解析度重建、...
《Contourlet變換》是科學出版社2008年04月出版的圖書。...... 本書可供計算機專業的本科生、研究生參考閱讀,旨在幫助讀者透徹理解和掌握Contourlet變換與方向濾波器組...
Contourlet變換——影像處理套用 林立宇,張友焱,孫濤,秦前清 編著 科學出版社 2008年4月出版 定價:40.00 語種:中文 標準書號:978-7-03-021200-9 裝幀:平裝...
《SAR圖像處理方法:Contourlet域隱馬爾可夫模型的套用》主要論述Contourlet域隱馬爾可夫模型的基本理論、方法和遙感套用,系統地介紹了Contourlet變換、Contourlet域隱馬爾可夫...
4.5基於Contourlet變換圖像去噪 4.5.1算法模型 4.5.2數值實驗 4.6基於Contourlet變換圖像增強 4.6.1算法模型 4.6.2數值實驗 4.7小結 第5章邊緣導向圖像壓...
第7章介紹Bandelet變換和套用。第8章介紹小線變換。第9章介紹Contourlet變換及其套用。第10章介紹脈衝耦合神經網路(PCNN)與小波變換。 本書以精縮的理論知識、實踐...
第十三章基於馬爾可夫模型與Contourlet變換的圖像超解析度復原算法 13.1算法的基本原理 13.2Contourlet係數塊結構 13.3馬爾可夫模型 13.4基於MRF模型和Cotourlet...
4.4 基於Contourlet變換的圖像融合算法 39 [1] 4.4.1 基於Contourlet變換的圖像融合框架 394.4.2 融合規則 404.4.3 實驗結果與分析 414.5...
基於機率模型的非下採樣Contourlet變換圖像去噪. 西北大學學報(自然科學版). 2009,39(1):13-18. [11] 賈建,陳莉. 基於雙變數模型和非下採樣Contourlet變換的...
研究現狀及難點,金字塔變換、小波變換、多小波變換、Curvelet變換、Contourlet變換的基本理論及基於各變換的圖像融合算法,多尺度邊緣表示理論及基於多尺度邊緣的圖像融合...
4.2 離散餘弦變換 4.3 離散哈特利變換 4.4 方波型變換 4.5 基於特徵分析的變換 4.6 小波變換 4.7 Radon變換 4.8 Contourlet變換 參考文獻 第5章 數字圖像的預處理...
