Braess悖論

布雷斯悖論（Braess 悖論）是交通網路流理論中的一個概念，指在司機獨立選擇最短路徑通行的情況下，開通某些路段反而導致整個交通網路出現擁堵，通行能力下降的現象。Braess 悖論是博弈論中的納什均衡概念在交通分配理論中的體現。

基本介紹

• 中文名：布雷斯悖論
• 外文名：Braess' paradox
• 學科背景：交通分配理論、網路流、博弈論
• 提出時間：1968年

基本介紹

Braess 悖論是由德國數學家迪特里希·布雷斯（Dietrich Braess）在 1968 年的一篇文章中提出的。Braess 悖論是指在個人獨立選擇路徑的情況下，為某路網增加額外的通行能力（如增加路段等），反而會導致了整個路網的整體運行水平降低的情況。有時在一個交通網路上增加一條路段，或者提高某個路段的局部通行能力，反而使所有出行者的出行時間都增加了，這種為了改善通行能力的投入不但沒有減少交通延誤，反而降低了整個交通網路的服務水平。人們對這個問題做過許多研究，在城市建設當中也儘量避免這種現象的發生。但在複雜的城市道路當中，Braess 悖論仍然不時出現，造成實際交通效率的顯著下降。若某道路系統的納什均衡並非最優狀態，就可能會產生 Braess 悖論現象。

案例分析

圖1中的交通網路給出了一個發生 Braess 悖論的例子。假設 AC 段和 BD 段路途較長，通行時間需要 25 分鐘；AD 段和 BC 段路途較短，但為堵車高發路段，通行時間為 5+x 分鐘，其中 x 為車流量。設有 10 個單位的車流量從 A 流向 B。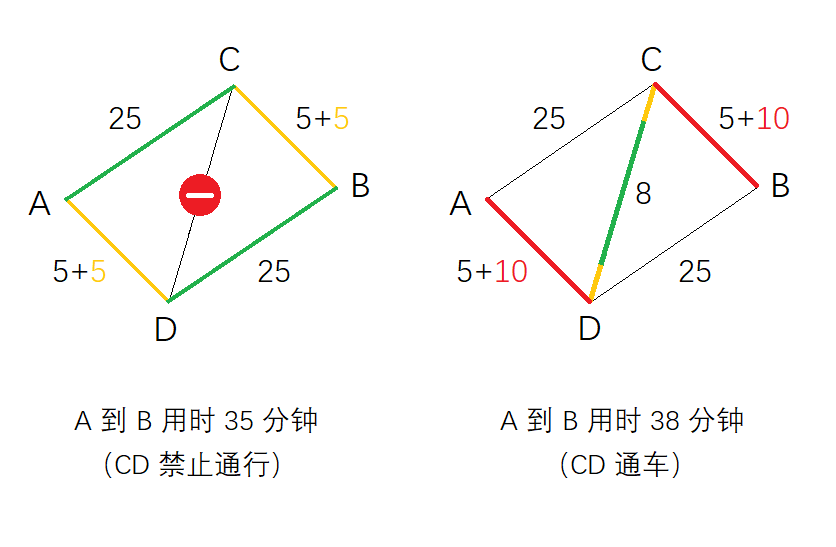

圖1 Braess 悖論的一個例子

當 CD 段禁止通行時，司機可以在 A→C→B 和 A→D→B 兩條路徑中選擇。在納什均衡下，兩條路徑各分配 5 個單位的車流量，因而 AD 段和 CB 段都需要 10 分鐘通行。不論走 A→C→B 還是 A→D→B，所需時間都是 35 分鐘。如果兩條路徑所分車流不均等，則車流較多的一邊通行緩慢，致使後面的司機轉而選擇車流較少的一邊通行。所以車流均分是此情形下的納什均衡。

增開一條通行時間僅為 8 分鐘的高速路段 CD 以後，就把以上的均衡打破了。因為走 A→D→C 快於走 A→C，走 D→C→B 也快於走 D→B。所以新的納什均衡是全部的 10 個單位車流都走 A→D→C→B 的路徑，造成 AD 段和 CB 段出現擁堵，需要 15 分鐘通行。最終總通行時間反而增加為 38 分鐘。更重要的是，A→D→C→B 是每個司機站在個人角度看來的最優路徑。再也不會有一半的車流願意分流到 AC 和 BD。

從上面的例子可以看出，在修建像 CD 這樣的高速路段之前，必須充分考慮到其通車以後，給整個路網中的其它路段會造成怎樣的影響。如果造成其它路段出現擁堵，則會使整個路網通行能力反而下降。

電路仿真

用物理學中的電路可以對交通流中的 Braess 悖論現象進行仿真。在無源的純電阻電路中，不論電阻網路如何複雜，多接通一個電阻總是引起總電阻減小，因此不會發生 Braess 悖論。但是交通流是一個非線性系統，相當於電阻不是定值電阻，而是會隨電流改變而改變，因而當新接通的電阻改變了電流分配時，就可能發生 Braess 悖論。可以用有源電路或者非線性元件（例如齊納二極體）來實現電路中的 Braess 悖論現象。