Bhahha散射

量子電動力學中，巴巴散射（英文：BhaBha Scattering）是指電子-反電子的散射過程，其中伴隨有交換虛光子。巴巴散射的名稱來源於印度物理學家霍米·J·巴巴（Homi J. Bhbha）。

基本介紹

• 中文名：Bhahha散射
• 外文名：BhaBha Scattering
• 別名：巴巴散射
• 領域：量子力學

簡介

量子電動力學中，巴巴散射（英文：BhaBha Scattering）是指電子-反電子的散射過程，其中伴隨有交換虛光子：

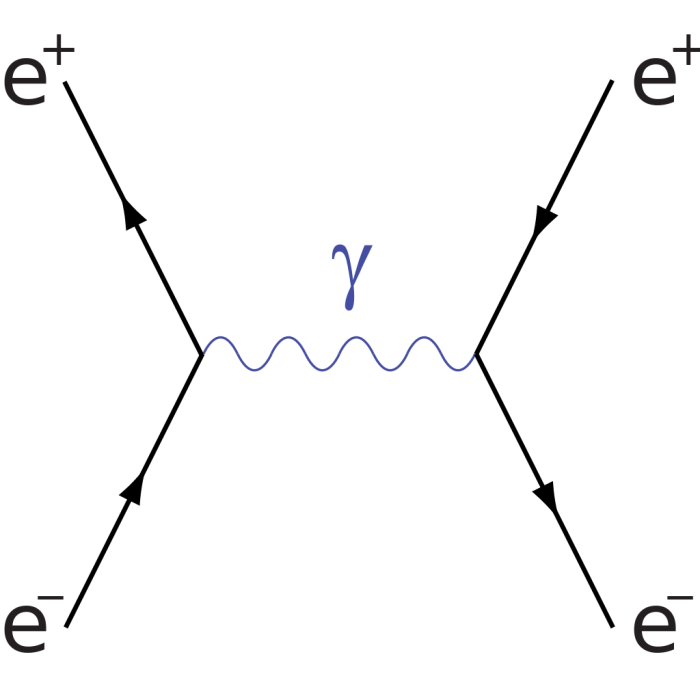
巴巴散射散射振幅的領頭項包含有兩個費曼圖的貢獻：一個是湮滅過程，一個是散射過程。巴巴散射的散射率在正負電子對撞機中被用來當作光度的監視指標。在經典電動力學中，巴巴散射實際就是正負電子通過庫侖力相互吸引的過程。

巴巴散射的名稱來源於印度物理學家霍米·J·巴巴（Homi J. Bhbha）。

散射微分截面

對自旋取平均的散射微分截面為：

這裡s，t和u是曼德爾斯坦變數， 是精細結構常數， 是散射角。散射截面的計算中忽略了電子的質量對碰撞的能量的貢獻，而只考慮了交換虛光子過程所做的貢獻。這個近似對於和Z玻色子的質量（約 ）相比很小的碰撞能量是成立的；對於相比不那麼小的碰撞能量，Z玻色子的交換過程所做的貢獻也要被考慮。

曼德爾斯坦變數

曼德爾斯坦變數定義為：

其中的近似在高能近似（相對論極限）中成立。

無偏振散射截面的推導

矩陣元

兩個費曼圖對散射矩陣的矩陣元都有貢獻。這裡用k和k'表示反電子的四維動量，用p和p'表示電子的四維動量，通過費曼圖的計算法則可得到由費曼圖給出的矩陣元：

其中是狄拉克矩陣，和是費米子的四分量旋量，和是反費米子的四分量旋量，參見狄拉克方程。注意到兩個過程的矩陣元相差一個負號。

矩陣元的平方

計算無偏振的散射截面時，需要對所有入射粒子的自旋取平均(自旋可能的值為s_e-和s_e+)，並且對所有出射粒子的自旋求和。即：

首先計算：

下面我們分別計算過程所包含的三項。

散射項

矩陣元的平方：

對自旋求和：

下面我們對四個粒子的所有自旋求和。這裡用s和s'來表示電子的自旋，r和r'來表示反電子的自旋。

這是解的精確形式，但在討論電子時一般都只考慮能量遠大於電子質量的情況，因此忽略電子質量從而得到下面的簡化形式：

湮滅項

湮滅項的計算過程與散射項類似；由於兩個費曼圖有交換對稱性，並且初始態和最終態的粒子完全相同，因此可以簡單地通過重新排列動量的位置得到結果：

最終解

對於干涉項所用的步驟相同，將三項加在一起從而得到的最終解為：

用途

巴巴散射在很多正負電子對撞實驗中用作對實驗光度的監測，精確的光度測量在精確的散射截面測量實驗中必不可少。

• 史丹福大學的大型Z玻色子探測器（Stanford Large Detector）在1993年進行的實驗中，小角度的巴巴散射被用來測量實驗的光度，測量的相對不確定度低於0.5%。
• 位於日本高能加速器研究機構的貝爾實驗，其前置量能器(Extreme Forward Calorimeter,[1])即是使用小角度的巴巴散射，來即時地量測該實驗的亮度，並且與中心碘化銫量能器所測得的大角度巴巴散射互動校正。貝爾實驗為目前亮度最高的B介子工廠。
• 正負電子對撞的實驗場所是地下的強子共振設備（ 能量約為1GeV至10 GeV），如北京的電子同步加速器（BES）、貝爾（Belle）實驗和介子的BaBar實驗，這些實驗利用大角度的巴巴散射作為光度測量的手段。如要達到相對不確定度小於0.1%的測量精確度，實驗測量需要和理論計算結果相比較，理論上要求計算到領導項及其下一個高階項的輻射修正。強子散射截面在這些較低能量下的高精度測量是理論計算μ子反常磁矩的關鍵條件之一，而計算μ子的反常磁矩能夠被用來約束超對稱以及其他超越標準模型的粒子理論。