基本介紹
- 中文名:B樹
- 外文名:B tree
- 別稱:B-樹、B_樹
- 提出者:R.Bayer和E.mccreight
- 提出時間:1970年
- 套用學科:計算機
- 適用領域範圍:軟體
- 適用領域範圍:編程
定義
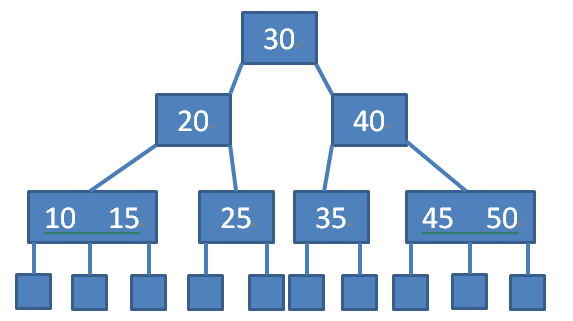 B樹
B樹性能分析
示例
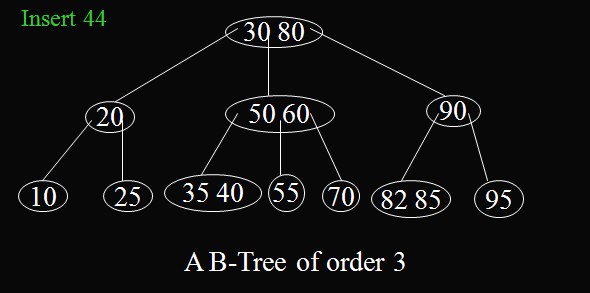 插入之前的B樹
插入之前的B樹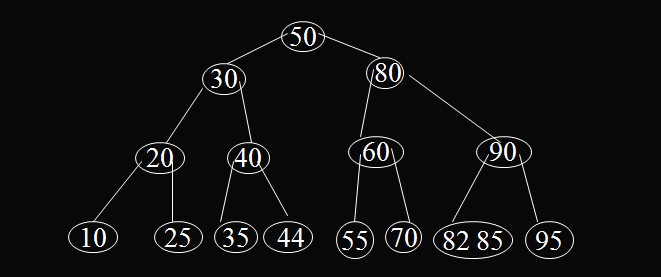 插入之後的B樹
插入之後的B樹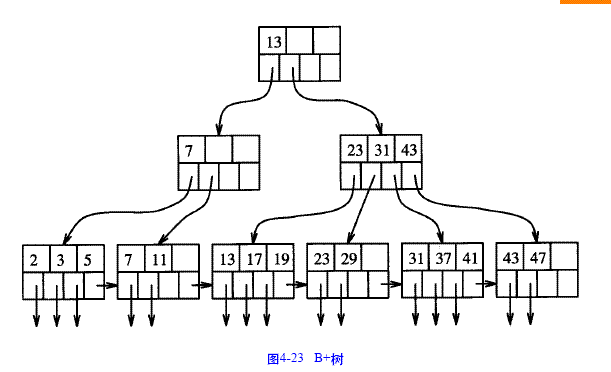
 B樹
B樹 插入之前的B樹
插入之前的B樹 插入之後的B樹
插入之後的B樹1970年,R.Bayer和E.mccreight提出了一種適用於外查找的樹,它是一種平衡的多叉樹,稱為B樹(或B-樹、B_樹)。 一棵m階B樹(balanced tree of order m)是一...
在計算機科學中,B樹(英語:B-tree)是一種自平衡的樹,能夠保持數據有序。這種數據結構能夠讓查找數據、順序訪問、插入數據及刪除的動作,都在對數時間內完成。B樹,...
B+樹與B樹最顯著的區別在於:B+樹只在葉節點存儲記錄,內部節點存儲關鍵碼值,這些關鍵碼值只是用於引導索引檢索位符,以為這B+樹的內部節點和葉節點在結構上有著...
B樹 Bitmap index 參考資料 1. Giampaolo, Dominic (1999). Practical File System Design with the Be File System (PDF). Morgan Kaufmann. ISBN 1-55860-...
其最最令人髮指的是二叉樹的高度太高。n叉樹的提出和實現解決了二叉樹的不足,典型的n叉樹有:2-3-4樹/紅黑樹和B樹。中文名 n叉樹 外文名 n-ary tree ...
它是在1972年由Rudolf Bayer發明的,當時被稱為平衡二叉B樹(symmetric binary B-trees)。後來,在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改為如今的“紅黑...
在計算機科學中,分形樹索引是一種樹數據結構,他保持數據排序,並允許在與B樹相同的時間內進行搜尋和順序存取,但插入和刪除的速度比B樹快。像B樹一樣,分形樹索引是...
R樹是一個高度平衡樹,它是B樹在k維上的自然擴展,用空間對象的MBR來近似表達空間對象,根據地物的MBR建立R樹,可以直接對空間中占據一定範圍的空間對象進行索引。 ...
2-3-4 樹在計算機科學中是階為4 的B樹。大體上同B樹一樣,2-3-4 樹是可以用做字典的一種自平衡資料結構。...
