B+樹

B+樹

B+ 樹是一種樹數據結構，通常用於資料庫和作業系統的檔案系統中。B+ 樹的特點是能夠保持數據穩定有序，其插入與修改擁有較穩定的對數時間複雜度。B+ 樹元素自底向上插入，這與二叉樹恰好相反。

基本介紹

  • 中文名：B+樹
  • 外文名：B+ Tree
  • 性質：樹數據結構
  • 特點：包含根節點、內部節點和葉子節點
簡介,節點結構,算法,查找,插入,刪除,註解,參見,

簡介

B+ 樹是一種樹數據結構，通常用於資料庫和作業系統的檔案系統中。B+ 樹的特點是能夠保持數據穩定有序，其插入與修改擁有較穩定的對數時間複雜度。B+ 樹元素自底向上插入，這與二叉樹恰好相反。
B+ 樹在節點訪問時間遠遠超過節點內部訪問時間的時候，比可作為替代的實現有著實在的優勢。這通常在多數節點在次級存儲比如硬碟中的時候出現。通過最大化在每個內部節點內的子節點的數目減少樹的高度，平衡操作不經常發生，而且效率增加了。這種價值得以確立通常需要每個節點在次級存儲中占據完整的磁碟塊或近似的大小。
B+ 背後的想法是內部節點可以有在預定範圍內的可變數目的子節點。因此，B+ 樹不需要象其他自平衡二叉查找樹那樣經常的重新平衡。對於特定的實現在子節點數目上的低和高邊界是固定的。例如，在 2-3 B 樹（常簡稱為2-3 樹）中，每個內部節點只可能有 2 或 3 個子節點。如果節點有無效數目的子節點則被當作處於違規狀態。
B+ 樹的創造者Rudolf Bayer沒有解釋B代表什麼。最常見的觀點是B代表平衡(balanced)，因為所有的葉子節點在樹中都在相同的級別上。B也可能代表Bayer，或者是波音（Boeing），因為他曾經工作於波音科學研究實驗室。

節點結構

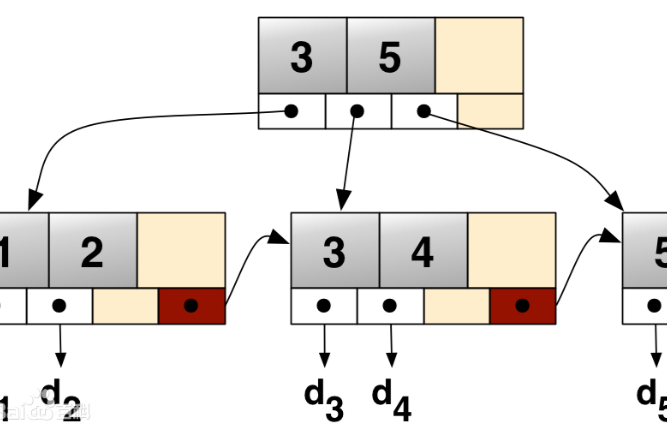
在 B+ 樹中的節點通常被表示為一組有序的元素和子指針。如果此B+樹的序數（order）是m ，則除了根之外的每個節點都包含最少
個元素最多 m-1 個元素，對於任意的節點有最多 m 個子指針。對於所有內部節點，子指針的數目總是比元素的數目多一個。因為所有葉子都在相同的高度上，節點通常不包含確定它們是葉子還是內部節點的方式。
每個內部節點的元素充當分開它的子樹的分離值。例如，如果內部節點有三個子節點（或子樹）則它必須有兩個分離值或元素a1和a2。在最左子樹中所有的值都小於等於a1，在中間子樹中所有的值都在a1和a2之間((a1，a2]），而在最右子樹中所有的值都大於a2。

算法

查找

查找以典型的方式進行，類似於二叉查找樹。起始於根節點，自頂向下遍歷樹，選擇其分離值在要查找值的任意一邊的子指針。在節點內部典型的使用是二分查找來確定這個位置。

插入

節點要處於違規狀態，它必須包含在可接受範圍之外數目的元素。
  1. 首先，查找要插入其中的節點的位置。接著把值插入這個節點中。
  2. 如果沒有節點處於違規狀態則處理結束。
  3. 如果某個節點有過多元素，則把它分裂為兩個節點，每個都有最小數目的元素。在樹上遞歸向上繼續這個處理直到到達根節點，如果根節點被分裂，則創建一個新根節點。為了使它工作，元素的最小和最大數目典型的必須選擇為使最小數不小於最大數的一半。

刪除

  1. 首先，查找要刪除的值。接著從包含它的節點中刪除這個值。
  2. 如果沒有節點處於違規狀態則處理結束。
  3. 如果節點處於違規狀態則有兩種可能情況：
  4. 它的兄弟節點，就是同一個父節點的子節點，可以把一個或多個它的子節點轉移到當前節點，而把它返回為合法狀態。如果是這樣，在更改父節點和兩個兄弟節點的分離值之後處理結束。
  5. 它的兄弟節點由於處在低邊界上而沒有額外的子節點。在這種情況下把兩個兄弟節點合併到一個單一的節點中，而且我們遞歸到父節點上，因為它被刪除了一個子節點。持續這個處理直到當前節點是合法狀態或者到達根節點，在其上根節點的子節點被合併而且合併後的節點成為新的根節點。

註解

假定L是節點允許擁有子節點的最小數目，而U是最大數目。則每個節點總是有在L和U之間（包含它們在內）個子節點，除了一個例外：根節點有從2到U（包含它們在內）個子節點。換句話說，根節點豁免於低邊界限制，而擁有它自己的低邊界2。這允許樹持有小數目的元素。根有一個子節點沒有意義，因為附著在這個子節點上的子樹可以簡單的附著在根節點上。允許根節點沒有子節點也是不需要的，因為沒有元素的樹典型的表示為沒有根節點。
Robert Tarjan證明了均攤的分裂/合併數目是 2。

參見

相關詞條

熱門詞條

聯絡我們