基本介紹
- 中文名:B-樹
- 外文名:B-tree
- 屬於:數學概念
- 類型:多路搜尋樹
- 特性:關鍵字集合分布在整顆樹中
簡介,概述,變體,資料庫的問題,已排序檔案的查找時間,提升查找的索引,插入和刪除帶來的麻煩,B樹運用的理念,B樹的弊端,相關條目,
簡介
在計算機科學中,B樹(英語:B-tree)是一種自平衡的樹,能夠保持數據有序。這種數據結構能夠讓查找數據、順序訪問、插入數據及刪除的動作,都在對數時間內完成。B樹,概括來說是一個一般化的二叉查找樹(binary search tree),可以擁有多於2個子節點。與自平衡二叉查找樹不同,B樹為系統大塊數據的讀寫操作做了最佳化。B樹減少定位記錄時所經歷的中間過程,從而加快存取速度。B樹這種數據結構可以用來描述外部存儲。這種數據結構常被套用在資料庫和檔案系統的實現上。
概述
在B樹中,內部(非葉子)節點可以擁有可變數量的子節點(數量範圍預先定義好)。當數據被插入或從一個節點中移除,它的子節點數量發生變化。為了維持在預先設定的數量範圍內,內部節點可能會被合併或者分離。因為子節點數量有一定的允許範圍,所以B樹不需要像其他自平衡查找樹那樣頻繁地重新保持平衡,但是由於節點沒有被完全填充,可能浪費了一些空間。子節點數量的上界和下界依特定的實現而設定。例如,在一個2-3 B樹(通常簡稱2-3樹),每一個內部節點只能有2或3個子節點。
B樹中每一個內部節點會包含一定數量的鍵值。通常,鍵值的數量被選定在d和2d之間。在實際中,鍵值占用了節點中大部分的空間。因數2將保證節點可以被拆分或組合。如果一個內部節點有2d個鍵值,那么添加一個鍵值給此節點的過程,將會拆分2d鍵值為2個d鍵值的節點,並把中間值節點添加給父節點。每一個拆分的節點需要最小數目的鍵值。相似地,如果一個內部節點和他的鄰居兩者都有d個鍵值,那么將通過它與鄰居的合併來刪除一個鍵值。刪除此鍵值將導致此節點擁有d-1個鍵值;與鄰居的合併則加上d個鍵值,再加上從鄰居節點的父節點移來的一個鍵值。結果為完全填充的2d個鍵值。
一個節點的分支(或子節點)的數量會比存儲在節點內部鍵值的數量大1。在2-3 B樹中,內部節點將會存儲1個鍵值(帶有2個子節點)或2個鍵值(帶有3個子節點)。一個B樹有時會被描述為2d+1。
一個B樹通過約束所有葉子節點在相同深度來保持平衡。深度在元素添加至樹的過程中緩慢增長,而整體深度極少地增長,並導致所有葉子節點與根節點距離加1。
在存取節點數據所耗時間遠超過處理節點數據所耗時間的情況下,B樹在可選的實現中擁有很多優勢,因為存取節點的開銷被分攤到裡層節點的多次操作上。這通常出現在當節點存儲在二級存儲器如硬碟存儲器上。通過最大化內部裡層節點的子節點的數量,樹的高度減小,存取節點的開銷被縮減。另外,重新平衡樹的動作也更少出現。子節點的最大數量取決於,每個子節點必需存儲的信息量,和完整磁碟塊的大小或者二次存儲器中類似的容量。雖然2-3 樹更易於解釋,實際運用中,B樹使用二級存儲器,需要要大量數目的子節點來提升效率。
變體
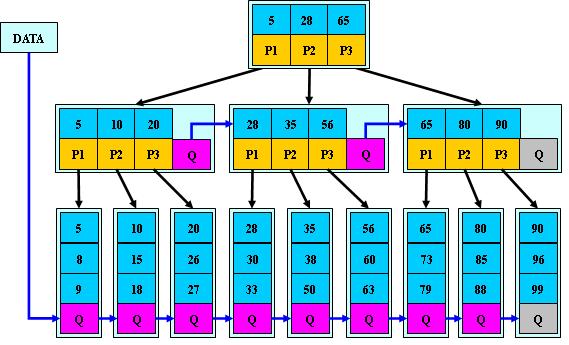
在B+樹,這些鍵值的拷貝被存儲在內部節點;鍵值和記錄存儲在葉子節點;另外,一個葉子節點可以包含一個指針,指向另一個葉子節點以加速順序存取。
B*樹分支出更多的內部鄰居節點以保持內部節點更密集地填充。此變體要求非根節點至少2/3填充,而不是1/2。為了維持這樣的結構,當一個節點填滿之後將不會再立即分割節點,而是將它的鍵值與下一個節點共享。當兩個節點都填滿之後,分割成3個節點。
計數B樹存儲,每一樹都帶有一個指針和其指向子樹的節點數目。這就允許了以鍵值為序快速查找第N筆記錄,或是統計2筆記錄之間的記錄數目,還有其他很多相關的操作。
資料庫的問題
已排序檔案的查找時間
通常,排序和查找算法會被通過大O符號,刻畫為比較級別的數值。對一個有N筆記錄的已排序表進行二叉查找,打個比方說,可以在O(log2N)比較級完成。如果表有1,000,000筆記錄,那么定位其中一筆記錄,將在20 個比較級內完成。 log21,000,000 = 19.931...
大資料庫一直以來被存儲在磁碟。從磁碟上讀取一筆記錄,與之後的比較鍵值操作相比,在花費的運行時間上前者處於支配地位。從磁碟讀取記錄的時間涉及到一個 尋道時間 和 旋轉延遲。尋道時間可能是從0到20或者更多毫秒,旋轉延遲平均下來約是旋轉周期的一半。對於一個7200 轉每分鐘的磁碟,旋轉周期大約是8.33毫秒。像希捷ST3500320NS這樣的磁碟,磁軌至磁軌的尋道時間為 0.8毫秒,平均讀取尋道時間為8.5毫秒。為了簡化,假設從磁碟讀取花費10毫秒。
樂觀來說,如此,在一百萬中定位一筆記錄將會話花費20次磁碟讀取乘上10毫秒每次讀取時間,總共是0.2秒。
時間花費沒有那么糟糕的原因是,獨立的記錄被成組地記錄在磁碟塊上。一個磁碟塊可能為16 千位元組。如果每筆記錄大小為160 位元組,那么一個塊可以存儲100 筆記錄。上面假設的磁碟讀取時間確切地說是讀取一個完整塊的時間。一旦磁頭到達位置,一個或者更多的磁碟塊可以以較小的延遲來完成讀取。對於100筆記錄每塊,最後差不多6個比較級是不需要任何磁碟讀取的————都在上次讀取操作中完成了。
為進一步加速查找,開始的13或14個比較級(每個需要一次磁碟訪問)必須要提速。
提升查找的索引
較大程度上的提升是通過索引來做到的。在上面的例子中,初始磁碟讀取從2個因素限制了查找範圍。這基本上可以通過創建一個輔助索引來改善,這個索引包含每塊磁碟塊上的首筆記錄(有時稱為稀疏索引)。這個輔助索引可能只有原始資料庫的1%大小,但是它可以更快速地被檢索。在輔助索引中查找入口可以告訴我們在主資料庫中要讀去哪一塊;查找輔助索引之後,我們只需要讀取主資料庫中的特定的某一個磁碟分塊————通過一次磁碟讀取開銷。索引可以提供10,000入口,所以,這樣最多需要14個比較級。就像主資料庫,輔助索引中最後6個左右的比較級可能在相同的磁碟分塊上。索引可以在大約8次磁碟讀取中完成查找,目標記錄會在9次磁碟讀取後獲得。
創建輔助索引的竅門是可以重複地給輔助索引創建輔助索引。那樣可以實現一個只擁有100 入口,能填滿一整個磁碟塊的輔助-輔助索引。
要找到想要的記錄,我們只需要讀取3次磁碟分塊,而不是14次。讀取和查找輔助-輔助索引中第一個(而且是唯一的)塊,標記了相應的輔助索引中的分塊。讀取和查找輔助索引的分塊,標記了主資料庫中相應的分塊。我們只需要30毫秒,而不是150毫秒就能獲取記錄。
輔助的索引,使得查找問題從約為log2N 磁碟讀取開銷的二分查找,變成logbN 磁碟讀取開銷的查找,其中b為分塊因素(每分塊的入口數目:b = 100 入口每分塊;logb1,000,000 = 3 次讀取)。
在實際中,如果主資料庫被頻繁查找,輔助-輔助索引和大部分的輔助索引可能會存儲在磁碟快取中,所以它們不會產生磁碟讀取。
插入和刪除帶來的麻煩
如果資料庫不會改變,那么編制索引就很簡單,而且索引永遠不需要改變。如果他們會改變,那么管理資料庫及其索引就變得非常麻煩。
從資料庫中刪除記錄不會引起太大問題。索引可以保持不變,記錄只需要標記為已刪除。資料庫仍然保持有序狀態。如果會有很多刪除,之後查找和存儲就不再那么高效了。
在一個有序檔案中進行插入將是個災難,因為需要給插入的記錄製造空間。在檔案中第一筆記錄後插入記錄需要把所有記錄向後偏移一個位置。如此的操作在實際中實在太過昂貴。
一種做法是預留一些空間給插入操作。磁碟塊有一些空閒空間允許後來的插入,而不是高密度地填充。這些記錄可以被標記為像是已刪除的記錄。
現在,只要塊中存在空間,插入和刪除都可以很快速。如果一個插入操作在一個塊上找不到合適的空間,就在臨近的塊中尋找,且要調整輔助索引。期望是臨近存在足夠的空間,以免重新調整大量的塊。作為可選方案,可以使用一些非排序的塊。
B樹運用的理念
B樹使用了以上所有的想法。特別是:
- 保持鍵值有序,以順序遍歷
- 使用層次化的索引來最小化磁碟讀取
- 使用不完全填充的塊來加速插入和刪除
- 通過優雅的遍歷算法來保持索引平衡
另外,B樹通過保證內部節點至少半滿來最小化空間浪費。一棵B樹可以處理任意數目的插入和刪除。
B樹的弊端
- 除非完全重建資料庫,否則無法改變鍵值的最大長度。這使得許多資料庫系統將人名截斷到70字元之內。