龐加萊極限是天體力學術語。
基本介紹
- 中文名:龐加萊極限
- 外文名:Poincare limit
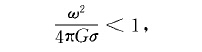
龐加萊極限是天體力學術語。
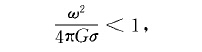
龐加萊極限是天體力學術語。龐加萊極限,天體力學術語.是流體自轉平衡時必須滿足的一個條件:其中。為流體自轉角速度,G是萬有引力常數,。為流體密度....
龐加萊的兩個堂兄弟是法國政界的著名人物:雷蒙·龐加萊是法蘭西學院院士,並於1913-1920年間任法國總統;呂西·龐加萊曾任法國民眾教育與美術部長,負責中等教育工作。因為視力極差,所以龐加萊在音樂和體育課上表現一般,除此之外,龐加萊在各方面都稱得上是成績優異。龐加萊的數學才華在上大學之前已經顯現出來。
龐加萊-本迪克松定理(Poincaré-Bendixson theorem)是平面定性理論的經典成果並是後續研究的重要基礎。給定系統dx/dt=X(x),(1),或平面系統:dx/dt=P(x,y),dy/dt=Q(x,y),(2),龐加萊-本迪克松定理斷言:若系統(2)的一條正半軌保持在某一不含奇點的有界區域內,則它盤旋逼近於一條極限環(它在該軌...
英語:Circle Limit IV)是M. C. 埃舍爾(M. C. Escher,又譯艾雪)在1960年7月完成的木刻版畫。是艾雪一系列圓極限題作的四樣作品的其中之一,表達了對於龐加萊所描述的雙曲空間的感受荷蘭數學物理學家布魯諾·恩斯特稱它是“最好的四個”,其中圓極限IV被認為是埃舍爾最具有大師風範的作品之一。
對於平面定常系統 ,極限集理論有甚為清晰完整的結論,可歸結如下:若系統的一條正半軌φτ(x0)(t≥0)保持在有界區域D內,則Lω(x0)必屬於下列情形之一: 1一個奇點; 2一條閉軌; 3一條奇閉軌。 由此即可推出龐加萊-本迪克松定理。 [1] 定性理論 播報 編輯 ...
這樣普恩加萊一步步把法國推向戰爭,普恩加萊的堂兄亨利·龐加萊曾稱他為“戰爭的普恩加萊”,這一綽號後來被大家接受並廣為流傳。他不惜一切代價,動員各方面力量,堅決把戰爭進行到底。為了使全國各政治派別團結一致共同對敵,普恩加萊實行”神聖同盟政策”,在他的政府中,包含了各種政治力量,例如原先的社會主義者...
這是最簡單的理論模型。它研究密度均勻的不可壓縮流體在均勻自轉時的平衡形狀及其穩定性問題(即偏離平衡形狀很小時,是否會破壞平衡)。設σ 為流體密度、ω為自轉速率、G為萬有引力常數,龐加萊求得產生平衡形狀的必要條件為: 。Ω=1的條件稱為龐加萊極限 對於密度不均勻的流體,此條件仍然成立,只是σ 表示整個...
變成另一個流),則被二截斷而成的兩條軌道,一個P+穩定(其。極限集為x),另一為P一穩定(其a極限集為x).對於半流和離散半動力系統只有P穩定軌道.泊松穩定軌道有時又稱為回復軌道,特別是在離散情形,這種稱謂更為多見(參見“回復軌道”).泊松穩定軌道是龐加萊(Poincare, (J.-)H. )於1899年引人的.
在這方面,從19世紀下半期到20世紀的最初十年,世界上許多著名數學家如黎曼(Riemann,G.F.B.)、克萊因(Klein,(C.)F.)、龐加萊(Poincaré,J.-H.)、施瓦茲(Schwarz,H.A.)、諾伊曼(Neumann,C.G.)和克貝(Koebe,P.)等人都做出了重要貢獻。發展歷史 以複數為係數的二元不可約多項式構成的方程P(z,w)...
法國著名數學家龐加萊(1854—1912)於1900年在巴黎召開的國際數學家會議上誇耀道:“現在可以說,(數學)絕對的嚴密性是已經達到了”。然而,事隔不到兩年,英國著名數理邏輯學家和哲學家羅素(1872—1970)即宣布了一條驚人的訊息:集合論是自相矛盾的,並不存在什麼絕對的嚴密性!史稱“羅素悖論”。1918年,...
龐加萊 如果歐幾里得幾何未能激起你少年時代的熱情,那么,你就不是一個天生的科學思想家。 ——愛因斯坦 純粹幾何學的學說往往會給出,而在許多問題中會給出多個簡單而自然的辦法來泂察諸真理的來源,去揭露那連線它們的神秘鏈索,去使它們獨特地、明白地、完全地被認識。——卓斯拿斯(MichaelChasles1793-1880)考慮...
法國數學家龐加萊在19世紀末把n維流形定義為一種連通的拓撲空間,其中每一點都具有和n維歐氏空間同胚的鄰域(被稱為龐加萊流形),從而開闢了組合拓撲學的道路。對流形的深入研究集中在流形上的微分結構與組合結構的存在性、唯一性問題,微分結構與組合結構的關係,流形的各種意義下的分類等問題,20世紀50—60年代做出...
二十世紀初,複變函數論又有了很大的進展,維爾斯特拉斯的學生,瑞典數學家列夫勒、法國數學家龐加萊、阿達瑪等都作了大量的研究工作,開拓了複變函數論更廣闊的研究領域,為這門學科的發展做出了貢獻。複變函數論不但在其他學科得到了廣泛的套用,而且在數學領域的許多分支也都套用了它的理論。它已經深入到微分...
19世紀後期,法國大數學家龐加萊(Poincare,(J.-)H.)創立了常微分方程定性理論。其基本思想是從微分方程本身的特徵去設法推斷其解所具有的性質,這就要從一些具有特殊性質的特解著手,如對奇點、周期解、極限環,以及更一般地,對軌線的極限集等加以分析研究,在此基礎上就可能對常微分方程所確定的解的總體的大...
克萊因和亨利·龐加萊在他們關於自守函式的工作中曾經用到離散型的無限群,即不連續群。挪威數學家S.李在1883年關於連續群的文章中引進了無限連續群,他藉助於一種微分方程來定義這種群,所得的變換並不依賴於有限多個連續的參量,而是依賴於任意函式,這種無限群被稱為無限連續李群(見李群)。無限群論在20世紀初...
法國著名數學家龐加萊(1854—1912)於1900年在巴黎召開的國際數學家會議上誇耀道:“現在可以說,(數學)絕對的嚴密性是已經達到了”。然而,事隔不到兩年,英國著名數理邏輯學家和哲學家羅素(1872—1970)即宣布了一條驚人的訊息:集合論是自相矛盾的,並不存在什麼絕對的嚴密性,史稱“羅素悖論”。1918年,...
重要的不變集有ω極限集、α極限集、非遊蕩集和鏈回歸集等。動力系統 粗略地說,如果自然界中一些隨時間演變的體系,其各種狀態x所構成的集合X有與時間t相關的動態規律Фt(x)(-∞ 對動力系統的研究開始於19世紀末,1881年以後,法國數學家龐加萊開始的常微分方程定性理論的研究就可以看作是動力系統的創始。後來...
他引進了許多不變數:基本群、同調、貝蒂數、撓係數,探討了三維流形的拓撲分類問題,提出了著名的龐加萊猜想。拓撲學的另一淵源是分析學的嚴密化。實數的嚴格定義推動康托爾從1873年起系統地展開了歐氏空間中的點集的研究,得出許多拓撲概念,如聚點(極限點)、開集、閉集、稠密性、連通性等。在點集論的思想影響...
在馬爾可夫鏈被提出之後,保羅·埃倫費斯特(Paul Ehrenfest)和Tatiana Afanasyeva在1907年使用馬爾可夫鏈建立了Ehrenfest擴散模型(Ehrenfest model of diffusion)。1912年亨利·龐加萊(Jules Henri Poincaré)研究了有限群上的馬爾可夫鏈並得到了龐加萊不等式(Poincaré inequality)。1931年,安德雷·柯爾莫哥洛夫(...
保測變換的各種回歸性質也是與遍歷性有關的重要研究課題。早在1912年(J.-)H.龐加萊就已證明了以下簡單而普遍的回歸定理:對於機率空間的保測變換φ,從一個正測度集合中出發的幾乎所有軌道都要無窮多次地返回這一集合。近年來關於回歸性質的研究成果有多重回歸定理等。定理推廣 繼伯克霍夫和馮·諾伊曼的開創性...
① 林斯泰特-龐加萊方法 它原用於天體力學。例如對方程:設其中當A,α是常數時,它是的解。若直接以x的式子代入方程,並使ε的各次冪的係數分別為零,以求(x)i(t),便會得到形如tmsin(nω0t)及tmcos(nω0t)的項,即所謂長期項(也稱永年項),長期項的出現大大妨礙了級數於t→時的收斂。為了避免長期...
法國在19世紀一直是最活躍的數學中心之一,湧現出一批優秀人才,如J.-B.-J.傅立葉、S.-D.泊松、J.-V.彭賽列、A.-L.柯西、J.劉維爾、E.伽羅瓦、C.埃爾米特、C.若爾當、(J.-)G.達布、(J.-)H.龐加萊、J.(-S.)阿達馬。他們在幾乎所有的數學分支中都作出了卓越貢獻。法國革命的影響波及歐洲各國,...
19世紀以來高維研究興起,如閔科夫斯基空間就是三維歐氏空間加上時間變數的四維空間。1878年德國數學家G.康托爾證明了一條線段上的點能夠和正方形的點建立一一對應,1890年義大利數學家皮亞諾根據法國數學家若爾當的曲線定義構造出能填滿一個正方形的曲線,這些都使數學家認真考慮維數的定義。1912年法國數學家龐加萊給...
在大會上作報告的數學家共有4位:J.H.龐加萊(但他因病缺席,由J.弗蘭紐爾(Franel)替他宣讀論文)A.胡爾維茨(Hurwitz),C.F.克萊因,G.皮亞諾(Peano)。這次大會以J.H.龐加萊報告的《關於純分析和數學物理》及C.F.克萊因報告的《目前高等數學問題》著稱於世。第二屆 時間:1900年 地址:法國...
混沌確定系統是龐加萊在研究三體問題時第一次發現的。進一步研究表明,混沌是非線性動力系統的固有特性,是非線性系統普遍存在的現象。牛頓確定性理論能夠充分處理的多維線性系統,而線性系統大多是由非線性系統簡化來的。混沌現象是自然界中的普遍現象,天氣變化就是一個典型的混沌運動。混沌現象的一個著名表述就是蝴蝶...
最早論及同倫群的是法國數學家儒勒·昂利·龐加萊,他於1895年引進的復形基本群被稱為第一同倫群。1912年荷蘭數學家布勞威爾引入同維流形之間映射的度以研究同倫分類,開創不動點理論。20世紀20年代德國數學家霍普夫探討了球面同倫理論。20世紀30年代波蘭數學家胡雷維奇建立了群的同倫理論,引進拓撲空間的n維同倫群。另一...
