齊次問題(Prouhet-Tarry problem)數論中的重要問題.用N (k)表示使方程組(A):x}+xz+…+x}=y+yz+…+ y,,…,才+式+…+對一丈+yz+"..+yl,在下述意義下為可解的最小整數t:x},xz}...}x, }yl}yz}...,y,都是正整數,但y,yz,"..}y不能是x‑xz,...,x,的重新排列.又用M(k>表示使方程組(A)為可解且使xk+i +xk+} +... +xk+yyk+}i z+靈+‘+…+少+‘成立的最小的t.有k+1鎮N(k>鎮M(k>,並用初等方法可證明N(k>鎮k (k+1)/2+1.對此問題,目前較好的結果是:當2林時,N(k>鎮(k2+3)/2,當2}k時,N(k)}(k2+4)l2;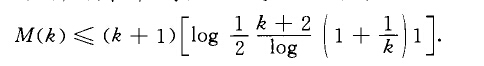
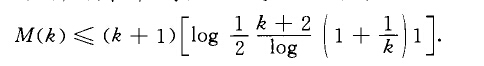
後者是由華羅庚於1938年得到的.關於上述兩個問題,至今還沒有完全解決.
