點到直線距離是連線直線外一點與直線上各點的所有線段中,垂線段最短,這條垂線段的長度。目標在於通過對點到直線距離公式的推導,提高學生對數形結合的認識,加深用“計算”來處理“圖形”的意識。
基本介紹
- 中文名:點到直線距離
- 外文名:Distance from a point to a line
- 主體:連線直線外一點與直線上各點
- 特點:垂線段最短
- 斜率:-A/B
公式整理

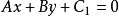

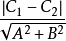

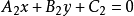


知識與技能目標:
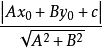

證明方法

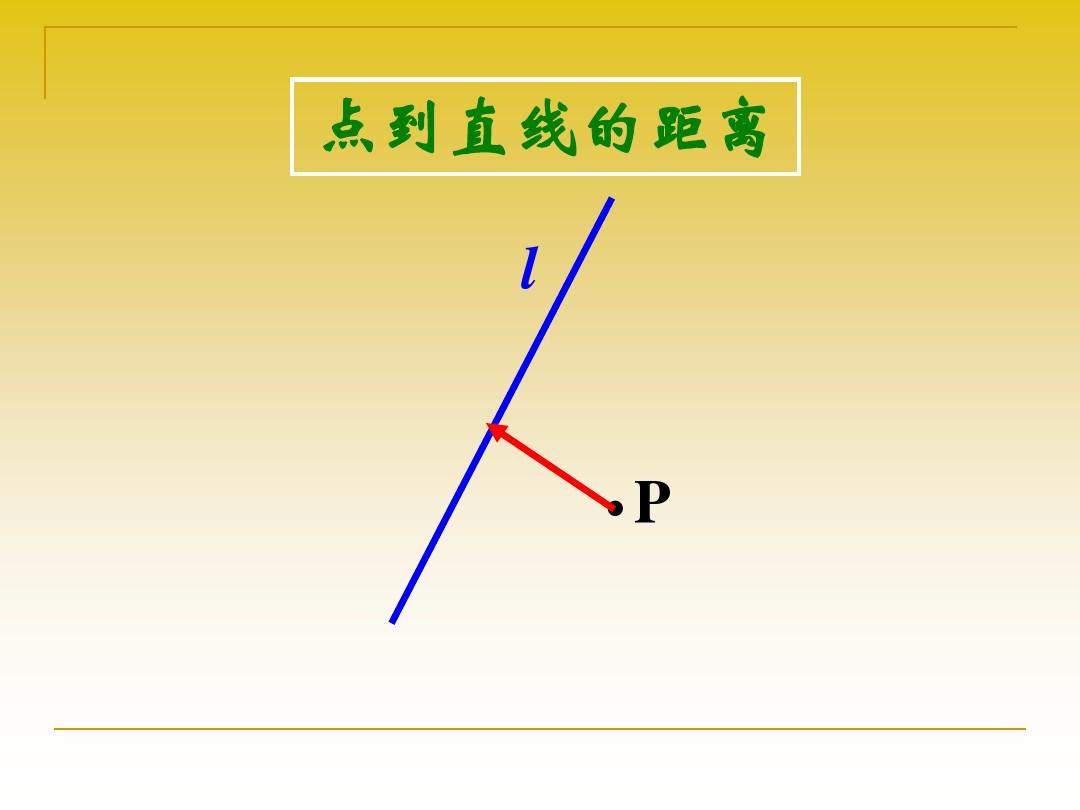
點到直線距離是連線直線外一點與直線上各點的所有線段中,垂線段最短,這條垂線段的長度。目標在於通過對點到直線距離公式的推導,提高學生對數形結合的認識,加深用“計算”來處理“圖形”的意識。

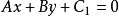

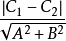

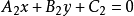


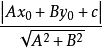


點到直線距離是連線直線外一點與直線上各點的所有線段中,垂線段最短,這條垂線段的長度。目標在於通過對點到直線距離公式的推導,提高學生對數形結合的認識,加深用...
一般情況下,點與直線的距離,是指點到直線的最短距離,即垂直距離。 [3] 在二維直角坐標中,直線 Ax+By+C=0 與點 (p,q) 的最短距離為...
▪ 點斜式 ▪ 斜截式 ▪ 截矩式 ▪ 兩點式 ▪ 法線式 ▪ 點方向式 3 距離計算 ▪ 點到直線距離 ▪ 兩平行線之間距離 直線...
定理一:任意兩條異面直線有且只有一條公垂線。定理二:兩條異面直線的公垂線段長(異面直線的距離)是分別連結兩條異面直線上兩點的線段中最短的一條。...
根據這一公式,求一點到一條直線的距離,只要先把這條直線的方程化成法線式,然後把已知點的坐標代入方程的左邊,計算所得值的絕對值,就是所求的距離。...
外(矢)距【external distance】指的是轉向點至圓曲線中點的直線距離。...... 外(矢)距【external distance】指的是轉向點至圓曲線中點的直線距離。...
當兩條直線相交所成的四個角中,有一個角是直角時,即兩條直線互相垂直,其中一條直線叫做另一直線的垂線,交點叫垂足。垂線段是一個圖形,點到直線的距離是一個...
圓心到弦的距離叫做弦心距。而弦心距公式是用於計算此距離的。有了這個公式,大大縮減了人們在解決有關圓問題的時間。...
③點到直線的距離:直線外一點到這條直線的垂線段的長度,叫做點到直線的距離。垂直向量垂直 編輯 在數學中,向量(也稱為歐幾里得向量、幾何向量、矢量),指具有大小...
