在一定溫度的平衡態下,氣體分子速率分布的統計規律,稱為麥克斯韋速率律。
基本介紹
- 中文名:麥克斯韋速率分布律
- 外文名:Maxwell speed distribution law
- 屬於:一個機率分布
- 提出者:麥克斯韋
- 特徵速率:最概然,平均,方均根速率
- 領域:統計學和物理
定義
































三個特徵速率
最概然速率


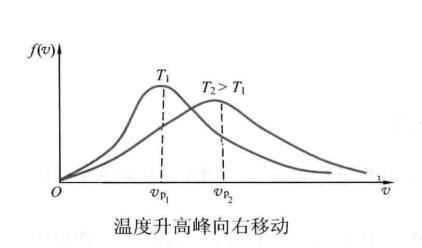 最概然速率
最概然速率平均速率


方均根速率


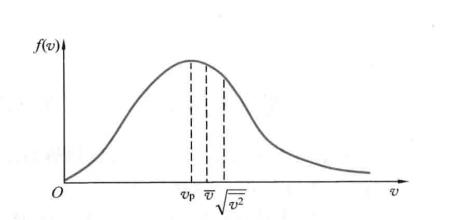 速率數量關係
速率數量關係在一定溫度的平衡態下,氣體分子速率分布的統計規律,稱為麥克斯韋速率律。


































 最概然速率
最概然速率



 速率數量關係
速率數量關係麥克斯韋在1859年用機率論證明了在平衡態下,理想氣體分子的速度分布是有規律的,這個規律稱為麥克斯韋速度分布律,並給出了它的分布函式表達式。...
在一定溫度的平衡態下,氣體分子速率分布的統計規律,稱為麥克斯韋速率律。...... 在一定溫度的平衡態下,氣體分子速率分布的統計規律,稱為麥克斯韋速率律。...
麥克斯韋速率分布曲線指的是麥克斯韋推論出的一種物理曲線。麥克斯韋速率分布曲線就是麥氏分布函式f(v)與速率v的函式關係曲線。它反映了在溫度為T的平衡態下,給定...
麥克斯韋速度分布定律函式式的推導 編輯 通過玻爾茲曼能量分布定律,我們很容易導出了分子按速度分布的函式式來,因為分子的動能與其速度之間有如下的關係:...
速率分布函式是一個描述分子運動速率分布狀態的函式。...... 速率分布函式麥克斯韋-玻爾茲曼分布 編輯 麥克斯韋-玻爾茲曼分布是一個描述一定溫度下微觀粒子運動速度的機率...
全同粒子在平衡態的統計分布律。獨立的定域子體系和經典極限的離域子體系中,在平衡態下N個全同粒子分布在其單粒子任一可及能級εi(i=1,2,3,…,為單粒子...
平衡態下,理想氣體分子速度分布是有規律的,這個規律叫麥克斯韋速度分布律。若不考慮分子速度的方向,則叫麥克斯韋速率分布律。所得的方程即為麥克斯韋速率方程。 ...
又稱“最可幾速率”,當氣體處於熱力學平衡態,分子符合麥克斯韋速率分布,與麥克斯韋速率分布f(v)的極大值對應的速率稱為最概然速率。...
玻爾茲曼分布律主要套用 編輯 玻爾茲曼分布律求典型速度 平均速度,最可能的速度(眾數)和均方根可以從麥克斯韋分布的性質獲得。 圖2 ...
麥克斯韋-玻爾茲曼分布具體說明了這個比例,對於任何速度範圍,作為系統的溫度的函式。它以詹姆斯·麥克斯韋和路德維希·玻爾茲曼命名。這個分布可以視為一個三維矢量的大小,...
麥克斯韋-玻爾茲受能量分布[1] 對於一個全同粒子體系,當獨立的定域子或經典...的活化分了分率顯著增加,因此溫度對反應速率的影響具有指數關係參考資料 1. ...
平均速率(average speed)是指物體運動的路程和通過這段路程所用時間的比,對運動...由麥克斯韋速度分布律得出的氣體分子三種特徵速率之一氣體分子熱運動的平均速率與...
麥克斯韋—波爾茲曼分布率(Maxwell-Boltz-mann distribution law)是全同粒子在平衡態的統計分布律。...
在精確驗證麥克斯韋速度分布律方面取得國際公認的重大成就;是中國制氧工業先驅,為國內制氧工業奠定了基礎;創建中國第一個雷達研究所,開拓了我國雷達的研究和套用;在...
平衡態時,氣體分子熱運動的速率分布服從麥克斯韋速率分布律,與速率分布函式的極大值對應的速率,曾稱最可幾速率,記作 。將速率分成相等的速率間隔,不同間隔內的...
4.2.5 方均根速率 4.3 能量均分定理和理想氣體內能 4.3.1 自由度 4.3.2 分子的自由度 4.3.3 能量均分定理 4.3.4 理想氣體內能 4.4 麥克斯韋速率分布律 4.4...
電子溫度是指電子運動產生動能同時溫度會改變。根據電子的平均動能,利用麥克斯韋速度分布律可以求出電子的溫度。...
12.9麥克斯韋麥克斯速率分布律Maxwell speed distribution law麥克斯韋速率速率分布律337 *12.10麥克斯韋麥克斯韋速率分布律麥克斯韋速率速率分布律的實驗驗證343 *12.11玻...
1860年麥克斯韋指出,氣體分子的頻繁碰撞並未使它們的速率趨於一致,而且出現穩定的分布。他利用機率統計方法導出了平衡態氣體分子的速率分布函式(稱為麥克斯韋分布)為:f...
1869年,他將麥克斯韋速度分布律推廣到保守力場作用下的情況,得到了玻爾茲曼分布律。1872年,玻爾茲曼建立了玻爾茲曼方程(又稱輸運方程),用來描述氣體從非平衡態到平衡...
4.3麥克斯韋速率分布律三種統計速率864.3.1麥克斯韋速率分布律864.3.2最概然速率、平均速率和方均根速率87*4.4氣體分子碰撞和平均自由程89...
這就是說,假若能夠精確測定任一時刻所有N個分子的速率的數值,則在一定的時間間隔內測得的氣體分子滿足麥克斯韋速度分布律的次數,將遠大於按其他速度分布的次數。當...
9.10麥克斯韋速率分布律的實驗驗證323*9.11玻耳茲曼分布律3249.12實際氣體等溫線326*9.13范德瓦耳斯方程327*9.14非平衡態輸運過程331提要335...
9.10麥克斯韋速率分布律的實驗驗證304 *9.11玻耳茲曼分布律305 9.12實際氣體等溫線307 *9.13范德瓦耳斯方程308 *9.14非平衡態輸運過程312 提要316 思考題318...
7.5麥克斯韋速率分布律7.6分子碰撞和平均自由程本章小結習題第8章熱力學基礎8.1熱力學第一定律8.2理想氣體的等體過程和等壓過程摩爾熱容...
9.10 麥克斯韋速率分布律的實驗驗證255?*9.11 玻耳茲曼分布律256提要258思考題259習題261科學家介紹 玻耳茲曼264第10章 熱力學第一定律67...
14.9 麥克斯韋速率分布律14提要17自測簡題18思考題18習題19第15章 熱力學第一定律2115.1 功 熱量 熱力學第一定律2115.2 準靜態過程2215.3 熱容24...
