麥克斯韋—波爾茲曼分布率(Maxwell-Boltz-mann distribution law)是全同粒子在平衡態的統計分布律。
基本介紹
- 中文名:麥克斯韋—波爾茲曼分布率
- 外文名:Maxwell-Boltz-mann distribution law
- 統計分布律:全同粒子在平衡態
- q :單粒子配分函式
概述
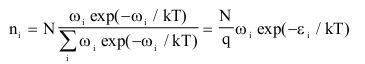 ①式
①式式中符號的意義
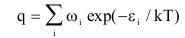 ②式
②式exp(- εi /kT)
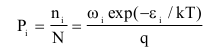 ③式
③式其他形式
 ④式
④式麥克斯韋—波爾茲曼分布率(Maxwell-Boltz-mann distribution law)是全同粒子在平衡態的統計分布律。
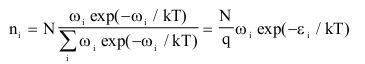 ①式
①式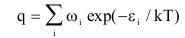 ②式
②式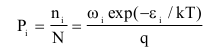 ③式
③式 ④式
④式麥克斯韋—波爾茲曼分布率(Maxwell-Boltz-mann distribution law)是全同粒子在平衡態的統計分布律。...
麥克斯韋-玻爾茲曼分布是一個描述一定溫度下微觀粒子運動速度的機率分布,在物理學和化學中有套用。最常見的套用是統計力學的領域。任何(巨觀)物理系統的溫度都是組成...
玻爾茲曼(L.E.Boltzmann)將麥克斯韋分布律推廣到有外力場作用的情況。在等寬的區間內,若E1>E2,則能量大的粒子數dN1小於能量小的粒子數dN2,狀態即粒子優先占據...
麥克斯韋—玻爾茲曼統計是描述獨立定域粒子體系分布狀況的統計規律。...... 麥克斯韋—玻爾茲曼統計是描述獨立定域粒子體系分布狀況的統計規律。所謂獨立定域粒子體系指的...
是描述獨立定域粒子體系分布狀況的統計規律。所謂獨立定域粒子體系指的是這樣一...因此所有經典粒子體系都是定域粒子體系,在近獨立假設下,都符合麥克斯韋-玻爾茲曼...
路德維希·玻爾茲曼1844年出生於奧地利的維也納,1866年獲得維也納大學博士學位。玻爾茲曼的貢獻主要在熱力學和統計物理方面。1869年,他將麥克斯韋速度分布律推廣到保守力場...
在統計力學中,麥克斯韋 - 玻爾茲曼統計量描述了熱平衡中不相互作用的材料顆粒在各種能態下的平均分布,並且當溫度足夠高或顆粒密度足夠低以使量子效應可忽略時適用。...
麥克斯韋—玻爾茲曼統計是描述獨立定域粒子體系分布狀況的統計規律。所謂獨立定域粒子體系指的是這樣一個體系:粒子間相互沒有任何作用,互不影響,並且各個不同的粒子...
這個規律也叫麥克斯韋速率分布律。麥克斯韋速度分布律歷史 編輯 1859年,J.C.麥克斯韋首先獲得氣體分子速度的分布規律,爾後,又為L.玻耳茲曼由碰撞理論嚴格導出。因此,...
玻耳茲曼能量分布律 學科 物理學 提出 玻耳茲曼 性質 能量分布定律 以玻耳茲曼認為麥克斯韋速度分布因子 中的 應當用 來替代,從這一觀點出發,玻耳茲曼計算出,分子...
在高溫和低密度條件下,費米-狄拉克分布過渡到經典的麥克斯韋-玻爾茲曼分布。費米-狄拉克分布歷史 編輯 1926年發現費米–狄拉克統計之前,要理解電子的某些性質尚較...
麥克斯韋-玻耳茲曼分布律正文 編輯 全同粒子在平衡態的統計分布律。獨立的定域子體系和經典極限的離域子體系中,在平衡態下個全同粒子分布在其單粒子任一可及...
1859年,J.C.麥克斯韋首先獲得氣體分子速度的分布規律,爾後,又為L.玻耳茲曼由碰撞理論嚴格導出。處於平衡狀態下的理想氣體分子以不同的速度運動,由於碰撞,每個分子的...
速率分布函式麥克斯韋-玻爾茲曼分布 編輯 麥克斯韋-玻爾茲曼分布是一個描述一定溫度下微觀粒子運動速度的機率分布,在物理學和化學中有套用。最常見的套用是統計力學的...
玻爾茲曼的貢獻主要在熱力學和統計物理方面。1869年,他將麥克斯韋速度分布律推廣到保守力場作用下的情況,把物理體系的熵和機率聯繫起來,闡明了熱力學第二定律的統計...
麥克斯韋—玻爾茲曼統計是描述獨立定域粒子體系分布狀況的統計規律。所謂獨立定域粒子體系指的是這樣一個體系:粒子間相互沒有任何作用,互不影響,並且各個不同的粒子...
下一段會提到,根據玻爾茲曼H定理,當允許分子碰撞時,這些分布並不穩定,並且會不可逆的最小化函式H(朝向麥克斯韋-玻爾茲曼分布) [1] 。...
如果布朗粒子相互碰撞的機會很少,可以看成是巨大分子組成的理想氣體,則在重力場中達到熱平衡後,其數密度按高度的分布應遵循玻耳茲曼分布(麥克斯韋-玻爾茲曼分布)。J....
1859年,麥克斯韋在克勞修斯工作的基礎上,提出了分子麥克斯韋速度分布率。這是物理學史上第一個統計定律。1871年,玻爾茲曼推廣了麥克斯韋的工作,提出了麥克斯韋–玻爾茲曼...
2.2.3 麥克斯韋一波爾茲曼分布定律(M-B統計)2.3 晶體熱振動的統計熱力學2.3.1 熱振動的能量2.3.2 熱振動熵和自由能2.4 磁性轉變的熱力學(鐵將二次固化!...
麥克斯韋—玻爾茲曼統計是描述獨立定域粒子體系分布狀況的統計規律。所謂獨立定域粒子體系指的是這樣一個體系:粒子間相互沒有任何作用,互不影響,並且各個不同的粒子...
