熱力學極限

熱力學極限是指粒子數（或體積）趨向無窮大時的極限。一般巨觀物體包含了10^23個粒子，可以認為是滿足熱力學極限的。

基本介紹

• 中文名：熱力學極限
• 外文名：Thermodynamic limit

套用

熱力學極限是一個統計物理中的常用假設，很多結論只有在熱力學極限下才會成立，例如：楊振寧和李政道證明相變只有在熱力學極限下才會發生；熵與能量等物理量的廣延性只有在熱力學極限下才成立。

熱力學極限也是玻爾茲曼統計的假設前提之一。

麥克斯韋-玻爾茲曼統計

麥克斯韋—玻爾茲曼統計是描述獨立定域粒子體系分布狀況的統計規律。

所謂獨立定域粒子體系指的是這樣一個體系：粒子間相互沒有任何作用，互不影響，並且各個不同的粒子之間都是可以互相區別的，在量子力學背景下只有定域分布粒子體系中的粒子是可以相互區分的，因此這種體系被稱為獨立定域粒子體系。而在經典力學背景下，任何一個粒子的運動都是嚴格符合力學規律的，有著可確定的運動軌跡可以相互區分，因此所有經典粒子體系都是定域粒子體系，在近獨立假設下，都符合麥克斯韋-玻爾茲曼統計。

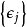因而符合麥克斯韋—玻爾茲曼統計分布的粒子，當他們處於某一分布（“某一分布”指這樣一種狀態：即在能量為的能級上同時有個粒子存在著，不難想像，當從巨觀觀察體系能量一定的時候，從微觀角度觀察體系可能有很多種不同的分布狀態，而且在這些不同的分布狀態中，總有一些狀態出現的幾率特別的大，而其中出現幾率最大的分布狀態被稱為最可幾分布）時，體系總狀態數為：

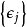
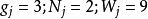
近獨立粒子統計力學

近獨立粒子統計指的是統計力學中對粒子的特定描述，它的特點是不考慮粒子間的相互作用。近獨立粒子三種主要模式是：

• 描述古典系統用：麥克斯韋-玻爾茲曼統計
  

• 描述含費米子的量子系統用：費米-狄拉克統計
  

• 描述含玻色子的量子系統用：玻色-愛因斯坦統計
  

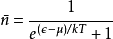
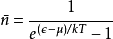
這三種統計的不同之處在於：

• 在古典物理中，粒子被視為能被區分出來的不同個體。
  
• 在量子物理中，兩個費米子不能處於同一個物理態。
  
• 在量子物理中，要區分玻色子只能從不同的物理態入手，位處同一態的玻色子沒有分別。因此，在物理態一的光子甲及在物理態二的光子乙，跟態一的光子甲及在態二的光子乙沒有分別。但在古典物理中它們會是兩個不同的系統，而在量子物理只算作一個。故玻色子表現得像它們都喜歡在同一狀態似的。
  

數學上使用可交換算符描述玻色子，反交換算符描述費米子，所以造成了以上的差別。