鬼場

在物理學中，法捷耶夫-波波夫鬼粒子（也稱為鬼場），是一種為了保持路徑積分表述的一致性而引入規範量子場論的附加場，以路德維希·法捷耶夫和維克多·波波夫的名字命名。

基本介紹

• 中文名：鬼場
• 外文名：Faddeev–Popov ghost
• 別稱：法捷耶夫-波波夫鬼粒子
• 領域：量子力學

費恩曼路徑積分表述的重複考慮

法捷耶夫-波波夫鬼粒子之所以是必須要引入的，是因為在路徑積分表述中，量子場論必須給出明確、非奇異的解，而由於規範對稱性的存在，我們無法從大量的因規範變換而相關的物理上等價的不同解挑選出唯一的解。這個問題起源於路徑積分重複考慮的規範對稱相關的場組態，這些其實對應於相同的物理態；路徑積分的測度包含一個係數，其不允許我們直接用一般的方法（例如費恩曼圖方法）從原始的作用量得到各種結果。但是，如果我們修改原始作用量，添加進去一個額外的場，打破規範對稱性，那么一般方法就可以使用了。這種場就叫做鬼場。這一方法被稱作“法捷耶夫-波波夫方法”（見BRST量子化）。這種鬼場只是一種計算工具，對外部來說並不對應於任何一種實際粒子：鬼粒子在費恩曼圖中只作為虛粒子出現——或者說，只對應於某些規範組態的缺失。但是它對於維持么正性是至關重要的。

描述鬼粒子的公式和其具體形式與所選擇的具體規範有關，但對於所有規範得到的實際結果是相同的。

量子場論

概述

在理論物理學中，量子場論（英語：Quantum field theory）是量子力學和狹義相對論相結合的物理理論，已被廣泛的套用於粒子物理學和凝聚態物理學中。量子場論為描述多自由度系統，尤其是包含粒子產生和湮滅過程的過程，提供了有效的描述框架。非相對論性的量子場論又稱量子多體理論，主要被套用於凝聚態物理學，比如描述超導性的BCS理論。而相對論性的量子場論則是粒子物理學不可或缺的組成部分。自然界目前人類所知的有四種基本相互作用：強相互作用，電磁相互作用，弱相互作用，引力。除去引力，另三種相互作用都找到了合適滿足特定對稱性的量子場論來描述。強作用有量子色動力學；電磁相互作用有量子電動力學，理論框架建立於1920到1950年間，主要的貢獻者為保羅·狄拉克，弗拉迪米爾·福克，沃爾夫岡·泡利，朝永振一郎，施溫格，理察·費曼和弗里曼·戴森等；弱作用有費米點作用理論。後來弱作用和電磁相互作用實現了形式上的統一，通過希格斯機制產生質量，建立了弱電統一的量子規範理論，即GWS（Glashow, Weinberg, Salam）模型。量子場論成為現代理論物理學的主流方法和工具。 而這些相互作用傳統上是由費曼圖來視覺化，並且提供簡便的計算規則來計算各種多體系統過程。

歷史

量子場論起緣於對量子躍遷所發出的光譜強度的計算。1925年馬克思·玻恩和帕斯庫爾·約當首先考慮了這個問題。1926年，馬克思·玻恩、沃納·海森堡和帕斯卡·約當運用正則量子化的方法，獲得了忽略極化和源項的自由電磁場的量子理論。1927年，保羅·狄拉克給出了這個問題的第一個自洽的解決方案。對當時人們唯一知道的經典場——電磁場——的量子化不可避免地導致了量子場論的出現，因為理論必須處理粒子數改變的情況，例如體系從只包含一個原子的初態變為包含一個原子和一個光子的終態。量子場論中，物質的質量僅被視為場的平方項之係數，並不具備實質物理意義。

顯然，對電磁場的量子化需要符合狹義相對論的要求。1928年約當和泡利證明，場算符的對易關係是洛倫茲不變的。1933年，尼爾斯·玻爾和Leon Rosenfeld將這些對易關係與測量類空間隔下的場的限制聯繫起來。狄拉克方程和空穴理論的發展促使人們將相對論中的因果性關係套用到量子場論中，並在Vladimir Fock工作的基礎上由Wendell Furry和羅伯特·奧本海默完成了這一工作。將量子力學和狹義相對論結合起來是促使量子場論發展的第二個動機。這條線索對於粒子物理及標準模型的發展很是關鍵。

1927年約當將對場的正則量子化方法推廣到量子力學中的波函式，並稱之為二次量子化。1928年約當和Eugene Wigner發現泡利不相容原理要求對電子場的量子化需要採用反對易的產生和湮滅算符。一致而且方便地處理多粒子系統的統計，是促使量子場論發展的第三個動機。這條線索進一步發展為量子多體理論，並對凝聚態物理和核物理產生了重要的影響。

BRST量子化

理論物理學中，BRST量子化是指以較嚴格的數學方式、藉由規範對稱性以量子化場論。在早期量子場論中，特別是非阿貝爾量子場論，其中的“鬼場”幾乎都是以重整化和反常抵消的方式處理。

70年代中期推出的BRST超對稱對量子場論進行計算時，合理引入法捷耶夫-波波夫鬼粒子，並從物理漸近狀態將其排除在外。至關重要的是，路徑積分得以防止引入可能破壞規範理論的項目。直到數十年後，物理學家才以BRST替代路徑積分的存在。

在20世紀80年代末，當量子場論得以解決低維流形拓撲結構的問題，BRST量子化變得比在利用以反常抵消解決鬼場的方法更有效。這種修改原始作用量，添加進去一個額外的場（鬼場）並打破規範對稱性的方法，即被稱作“法捷耶夫-波波夫方法”。至於規範不變性和BRST不變性之間的關係，使得哈密頓系統的狀態由粒子的規範量子化選擇。此外，在某些情況下，特別是重力和超引力，BRST必須由更一般的形式，例如以巴塔林-維爾可維斯基代數取代。

費曼圖

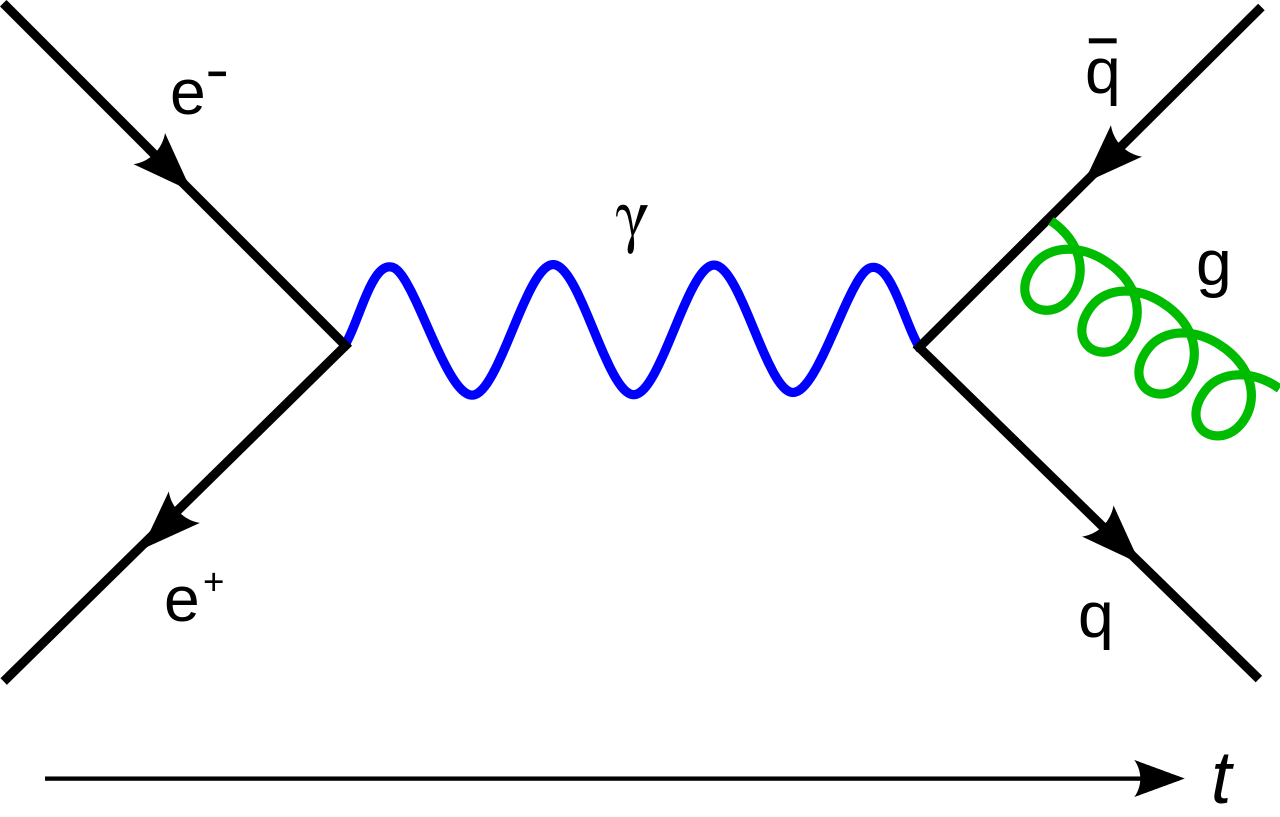
費恩曼圖（英語：Feynman diagram）是美國物理學家理察·費曼（即費恩曼）在處理量子場論時提出的一種形象化的方法，描述粒子之間的相互作用、直觀地表示粒子散射、反應和轉化等過程。使用費恩曼圖可以方便地計算出一個反應過程的躍遷機率。

在費恩曼圖中，粒子用線表示，費米子一般用實線，光子用波浪線，玻色子用虛線，膠子用圈線。一線與另一線的連線點稱為頂點。費恩曼圖的橫軸一般為時間軸，向右為正，向左代表初態，向右代表末態。與時間軸方向相同的箭頭代表正費米子，與時間軸方向相反的箭頭表示反費米子。

參見

• 巴塔林-維爾可維斯基代數
  
• 量子化