高爾投影屬任意性質的正軸割圓柱投影。設圓柱投影面與地球相割於南北緯30°(或50°),按球面透視法以等距離條件將經緯線網投影到圓柱面上,再沿一母線展成平面。這種投影圖,緯線為一組等距的平行直線,經線為一組與緯線垂直的等距平行直線,經緯線構成方格網。
基本介紹
- 中文名:高爾投影
- 外文名:Gall's projection
- 定位:任意性質的正軸割圓柱投影
- 方法:球面透視法
- 可用於:世界地圖
- 性質:地圖投影
概念,圓柱投影,透視法,經緯網,地圖投影,
概念
高爾投影屬任意性質的正軸割圓柱投影。設圓柱投影面與地球相割於南北緯30°(或50°),按球面透視法以等距離條件將經緯線網投影到圓柱面上,再沿一母線展成平面。這種投影圖,緯線為一組等距的平行直線,經線為一組與緯線垂直的等距平行直線,經緯線構成方格網。相割兩條緯線為標準線,無變形,沿經線長度與實地相等,面積與角度等變形線與緯線平行,變形值離相割緯線越遠則越大。可用於世界地圖。
圓柱投影
以圓柱面作為投影面,使圓柱面與地球相切或相割,將地球面上的經緯線投影到圓柱面上,然後把圓柱面沿一條母線剪開展為平面而成。由於圓柱面與地球相切或相割的位置不同,有正軸圓柱投影、橫軸圓柱投影和斜軸圓柱投影。正軸圓柱投影是圓柱的軸與地軸重合,橫軸圓柱投影是圓柱的軸與地軸垂直,斜軸圓柱投影是圓柱的軸與地軸斜交。正軸圓柱投影的經緯線形狀比較簡單,稱為標準網。緯線為平行直線,經線為與緯線垂直且間隔相等的平行直線。在這類投影圖上任意一點的位置是用直角坐標表示的。設以某一條經線為X軸,赤道為Y軸,由於緯線投影為平行於赤道的直線,所以X坐標僅依緯度的變化而變化,即X是緯度q的函式,一般用X=f(q)式表達。經線為與赤道垂直的平行直線,經線間的間隔與相應的經差λ成正比,故Y坐標與經差成正比,即y=cλ(c—常數)。因此正軸圓柱投影的一般公式為:
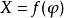
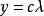
在圓柱投影中套用比較廣泛的是正軸等角圓柱投影,又名墨卡托投影。在這個投影圖上赤道是標準緯線,其他各緯線的長度比均大於1。為了保持等角特性,任一點的經線長度比均等於該點的緯線長度比,因此除赤道處經線長度比等於1之外,其他地方的經線長度比也隨緯度的增加而增大。例如在緯度60°地方,緯線與經線的長度比均為2,緯度80°地方,經線和緯線長度比均等於5.7。由於經線長度比隨緯度增高而增大,故圖上緯線間隔從赤道向兩極逐漸增大。極地不能表示出來。
墨卡托投影具有一個很重要的特性,就是把等角航線(又稱斜航線)表現為直線,所以它在編制航海圖和航空圖中被廣泛採用。例如我國編繪比例尺小於1∶2.5萬的海圖採用的是這個投影。此外,由於這個投影在低緯度地區變形小,而且經緯線形狀簡單,常用於繪製赤道附近的分國地圖。例如我國地圖出版社出版的一整套分國地圖中,沿赤道的分區地圖均採用這個投影。
透視法
指繪畫中將物體在空間的立體感再現於平面上的方法。分為線性透視法和空間顯示法兩大體系。前法又稱科學透視法,15世紀初義大利畫家馬薩喬首先套用在繪畫上。畫者靜止不動,須一隻眼睛盯視前方,根據光學和數學的原則,平面上所有物體的空間位置,如用線條圖示其輪廓及光的投影會消失在一、二個點上,分別稱平行透視(焦點透視)和成角透視(餘角透視)。這是人為性的科學法則,要求精確和嚴謹的數據,在繪畫中有利於表現物體的深度,但時常與美感有牴觸。後法指暗示空間的其他方法:1. 縱透視,離視者越遠的物體在畫面上的位置越高。2. 斜透視,除有縱透視特徵外,物體呈斜軸線直行以暗示後退。3. 依照物體與視點間的距離作大小、間隔的遞減,視點不固定,移動時參照這種關係構置畫面。以上三點在中國傳統畫中常被套用,稱為 “散點透視”。4. 重疊法。5.前縮法。6. 投影法。7. 立體表現。8. 隨物體遠近色彩產生變化的空間透視法等。
經緯網
由地球參考橢球面的經線和垂直於它的緯線構成縱橫交錯的、可作為地理坐標的經緯線網。在地球儀或地圖上,由經線和緯線相互交織的格網。它涵蓋地球表面上的任何部位,構成地理網狀坐標系。所有的經線長度都相等,所有的緯線之間都是平行的。地球上任何一個地方的位置都可以用一條經線和緯線的交叉點一組經緯度來表示。它在軍事、航空、航海、地質勘探等方面很有用處。
地圖投影
按照一定的數學法則將地球橢球面上的經緯線轉移到平面上的方法。也就是使地球橢球面上各點的地理坐標與平面上各點的直角坐標(或極坐標)保持一定的函式關係。地球橢球面是曲面,而地圖是繪製在平面上,因此製圖時首先要把曲面展為平面。然而地球橢球面是個不可展的曲面,假如把它直接展為平面,必然發生破裂或褶皺,用這種具有破裂或褶皺的平面繪製地圖,顯然是不實用的。所以必須採用數學方法將曲面展為平面,以保持平面上圖形的完整和連續。地圖投影方法很多,但不論採用什麼投影方法所得到的經緯線網形狀都不可能與地球橢球面上的經緯線網形狀完全相似。這表明投影之後地圖上的經緯線網發生了變形,因而根據地理坐標展繪在地圖上的各種地理事物也必然隨之產生變形。變形主要表現在三個方面: 長度變形、面積變形和角度變形。變形是不可避免的,但若給予一定的條件,如等角條件,等積條件,則可使其中某種變形等於零,用以滿足不同用途對地圖投影的要求。按變形性質地圖投影可分為三類: 等角投影、等積投影和任意投影(包括等距投影)。
地圖投影最初建立在透視的幾何原理上,它是把地球橢球面直接透視到平面上,或透視到可展為平面的曲面上,如圓柱面和圓錐面。這樣就得到具有幾何意義的方位、圓柱和圓錐投影。隨著科學的發展,為了使地圖上變形儘量減小,或者為了使地圖滿足某些特定要求,地圖投影逐漸跳出了原來藉助幾何面構成投影的框子,而產生了一系列按照數學條件構成的投影。按照構成方法可以把地圖投影分為兩大類: 幾何投影和非幾何投影。幾何投影是把地球橢球面上的經緯線投影到幾何面上,然後將幾何面展為平面而成的。根據幾何面的形狀可以分為方位投影、圓柱投影和圓錐投影。非幾何投影是不藉助於幾何面,根據某些條件用數學解析法確定地球橢球面與平面之間點與點的函式關係。在這類投影中,一般按經緯線形狀又分為偽方位投影、偽圓柱投影、偽圓錐投影和多圓錐投影。
