基本介紹
- 中文名：體積單位
- 外文名：unit of volume
- 學科：數理科學
- 類型：數學術語
- 重要性：體積的度量單位
- 體積：物件占有多少空間的量
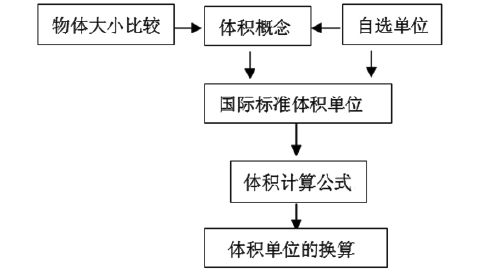
體積,基本單位,單位換算,中國古代計量單位,相關教學,
體積
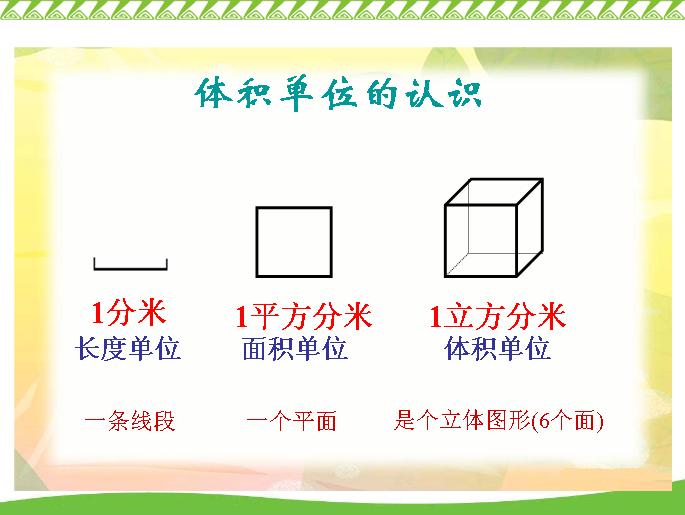
體積，幾何學專業術語，是物件占有多少空間的量。體積的國際單位制是立方米。一件固體物件的體積是一個數值用以形容該物件在三維空間所占有的空間。一維空間物件（如線）及二維空間物件（如正方形）在三維空間中都是零體積的。
中國，也是世界上最早得出計算球體積正確公式的是南朝數學家祖沖之，比歐洲人約早一千年。他還精心鑽研天算之術(指天文數學)，精治大明曆，經他再三請求，於510年得以正式頒行，他還製成銅日晷（一種用測日影的方法來計時的儀器）、漏壺等精密觀察儀器多種，為後世所取法。
基本單位
棱長是1毫米的正方體，體積是1立方毫米
棱長是1分米的正方體，體積是1立方分米
棱長是1米的正方體，體積是1立方米
單位換算
1立方米=1000升=1000立方分米=1，000，000毫升=1000000立方厘米=1，000，000，000立方毫米
1升=1立方分米=1000毫升=1000立方厘米=1，000，000立方毫米
1立方英尺=1（ft3）=0.0283立方米（m3）=28.317升（liter）=28.317立方分米（dm3）=28317立方厘米=28317000立方毫米
35.315立方英尺(ft)= 6.29桶(bbl)
1千立方英尺(mcf)= 28.317立方米(m3)
1百萬立方英尺(MMcf)=2.8317萬立方米(m3)
10億立方英尺(bcf)= 2831.7萬立方米(m3)
1萬億立方英尺(tcf)= 283.17億立方米(m3)
1立方英寸(in)= 16.3871立方厘米(cm3)
1英畝·英尺=1234立方米(m3)
1桶(bbl)= 0.159立方米(m3)= 42美加侖(gal)
1美加侖(gal)= 3.785升(l)
1美夸脫(qt)= 0.946升(l)
1美品脫(pt)= 0.473升(l)
1美吉耳(gi)= 0.118升(l)
1英加侖(gal)= 4.546升(l)
中國古代計量單位
1石（dàn） = 10斗（dǒu）
1斛（hú） = 本為10斗，後來改為5斗
1斗（dǒu） = 10升
1龠(yuè) = 0.5合（gě）
1升 = 10合（gě）
相關教學
體積概念的建立是學生空間觀念形成過程中的一次重要的飛躍，它標誌著兒童在“精細認識”二維空間的基礎上，開始“精細認識”三維空間。體積是對三維物體所占空間大小的一種度量，既然是度量，就離不開度量單位以及單位的個數。因此本單元教學一定要抓住“體積單位和數體積單位的個數”這條線，引導學生經歷多樣化的操作活動，理解概念本質，進一步培養學生的空間觀念與初步的推理能力。
為了實現這一目標，劉加霞等又重新研讀不同版本的教材，合理設計每一課時的教學內容，進一步明確“教什麼”。在此過程中我們又一次體驗到:“教什麼”遠比“怎么教”更重要。廣大一線教師必須認識到這一點。
通過對北師大版、人教版、蘇教版等版本教材的梳理和比較，可以看出五年級“長方體、正方體的體積”單元的教學內容整體編排結構相同，如右圖。
能不能創新性地重新斷課?能不能把“體積和體積單位”斷成兩節課?把“體積單位及其換算”作為一課時可以嗎?這樣是否能夠引導學生在充分的觀察、操作中建立起體積概念及體積單位的表象?又查閱其他版本的教材，西南師大版和青島版教材就把“體積單位的換算”放在“體積計算公式”之前，是藉助體積單位的堆積獲得換算關係的。這增加了劉加霞等重新編排教學內容的信心:更加重視體驗過程，推遲形式化計算公式的引入，有利於培養學生對體積單位的量感，發展空間觀念，還為探究體積計算做好鋪墊。
在分析各版本教材的基礎上，結合教學經驗，關於新教學內容的斷課我們進行了一些嘗試:第一課時，體積的認識;第二課時，體積單位及體積單位間的換算;第三課時，長方體、正方體的體積計算。這樣調整，目的是拉長學生對體積、體積單位的體驗過程，讓學生利用體積的意義、體積單位的堆積來獲得物體的體積。
這樣斷課，除了有利於體積單位表象的建立，同時數體積單位個數的活動經驗可以為接下來探究長方體體積公式做好準備，為深入理解體積、表面積等概念以及空間觀念培養奠定基礎。
