馬格努斯效應（Magnus Effect），以發現者馬格努斯命名， 流體力學當中的現象，是一個在流體中轉動的物體(如圓柱體）受到的力。
馬格努斯效應在球類運動項目中非常普遍，不僅僅是足球和桌球項目，在網球、棒球、排球、籃球等中都有套用，所以對馬格努斯效應的產生原因和在球類運動中的套用進行研究，對球類運動的教學水平、訓練效果和競賽成績有著重要的指導意義和實踐意義。
另外馬格努斯效應是一種非線性的複雜力學現象，深入研究其機理和規律將對旋轉彈丸、飛彈的設計、氣動性能分析以及制導控制起指導意義。
基本介紹
- 中文名：馬格努斯效應
- 外文名：Magnus Effect
- 別稱：馬格納斯效應
- 提出者：海因里希·馬格努斯
- 提出時間：1852年
- 套用學科：物理
- 適用領域範圍：體育、航海、航空、航天等
發現歷程,原理,舉例,球類運動的馬格努斯效應,旋轉彈丸的馬格努斯效應,旋轉飛彈的馬格努斯效應,套用,
發現歷程
這個效應是德國科學家H.G.馬格納斯於1852年發現的，故得名。在靜止粘性流體中等速旋轉的圓柱，會帶動周圍的流體作圓周運動，流體的速度隨著到柱面的距離的增大而減小。這樣的流動可以用圓心處有一強度為Γ的點渦來模擬。 於是馬格納斯效應可用無粘性不可壓縮流體繞圓柱的有環量流動來解釋（見有環量的無旋運動）。馬格納斯效應曾被用來藉助風力推動船舶航行，用幾個迅速轉動的鉛直圓柱體代替風帆。試驗是成功的，但由於不經濟，所以未被採用。足球、排球、網球以及桌球等的側旋球和弧圈球的運動軌跡之所以有那么大的弧度也是起因於馬格納斯效應。
在1852年德國物理學家海因里希·馬格努斯（Heinrich Magnus）描述了這種效應。然而早在1672年艾薩克·牛頓（Isaac Newton）在觀看了劍橋學院（Cambridge college）網球選手的比賽後描述和正確推斷了這種現象的原由。在1742年英國的一位槍炮工程師班傑明·羅賓斯（Benjamin Robins）解釋了在馬格努斯效應中步槍彈丸（musket balls）運動軌跡的偏差。
原理
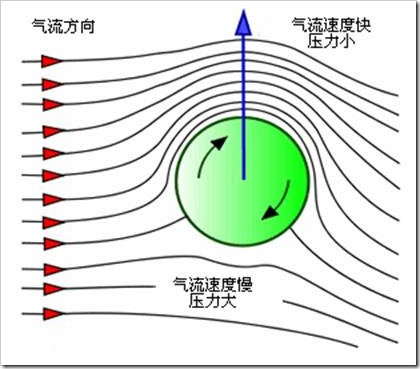
旋轉物體之所以能在橫向產生力的作用，是由於物體旋轉可以帶動周圍流體旋轉，使得物體一側的流體速度增加，另一側流體速度減小。
根據伯努利定理，流體速度增加將導致壓強減小，流體速度減小將導致壓強增加，這樣就導致旋轉物體在橫向的壓力差，並形成橫向力。同時由於橫向力與物體運動方向相垂直，因此這個力主要改變飛行速度方向，即形成物體運動中的向心力，因而導致物體飛行方向的改變。用位勢流理論解釋，則旋轉物體的飛行運動可以簡化為“直勻流+點渦+偶極子”的運動，其中點渦是形成升力的根源。在二維情況下，旋轉圓柱繞流的橫向力可以用儒可夫斯基定理來計算，即橫向力=來流速度 x 流體密度 x 點渦環量。
舉例
球類運動的馬格努斯效應
比如，足球在氣流中運動時，如果其旋轉的方向與氣流同向，則會在球體的一側產生低壓，而球體的另一側則會產生高壓。向前運動的球在以順時針方向旋轉時，下側由於迎著氣流運動，受到的空氣摩擦力會更大。這就得使足球下側受到的壓力比上側更大，足球在壓力的作用下便會朝上偏。如果足球以逆時針方向旋轉，則相反。
旋轉彈丸的馬格努斯效應
炮彈在飛行時，要受到空氣阻力的作用。阻力的方向與質心的速度方向相反，其合力不一定通過質心，阻力對質心的力矩就會使炮彈在空中翻轉，這樣，炮彈既飛不遠，還可能是彈尾先接觸目標而無法引爆，喪失戰鬥力。為了避免這種事故的發生，就在炮筒內壁刻上刻出來複線川，這樣就可以使炮彈在飛行時繞對稱軸高速旋轉，這種進動使得炮彈具有軸向穩定性，但此時將發生馬格努斯效應。
1852年，馬格努斯曾預言，當繞自身對稱軸旋轉的彈體以迎角飛行時，在旋轉和橫向繞流的共同作用下，彈體上將出現一個與迎角平面垂直的附加空氣動力，或人稱之為“馬格努斯力”。一般情況下，馬格努斯力與同一迎角下的法向力相比並不大，約為法向力的1~10%，但馬格努斯效應對彈丸的射擊精度有重要的影響。因為在彈丸飛行的全過程中，彈丸受到橫側方向上的一個非阻尼力，使飛行軌跡偏離射擊方向，同時馬格努斯力矩也常是引起動不穩定的重要因素。
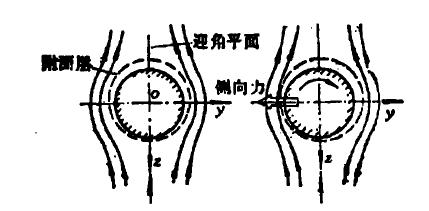
附面層的存在對外界有位流動的影響相當於固體邊界向外推移了一個位移厚度。彈體不旋轉時，附面層對稱於迎角平面，這樣由原來的彈體界面附加上附面層位移厚度得到的有效外形相對於迎角平面也是對稱的，不構成產生側向力的機理。但是，當彈體旋轉時，附面層由於粘性力的傳遞而畸變，如圖所示，左側變薄，右側變厚，最大厚度的位置不是在正上方，而移到了右側。這樣由原來的彈體界面附加上附面層位移厚度得到的有效外形相對於迎角平面不再是對稱的了。所以，可以斷定，由有效外形計算的空氣動力必然產生一個側向力。
旋轉飛彈的馬格努斯效應
許多小型飛彈，例如反坦克飛彈，在飛行過程中也要繞對稱軸旋轉，這樣做的目的有二:一、可以克服飛行中由於加工誤差而導致的氣動偏心:二、可以取得飛行中的穩定性，從而減少控制系統的通道數，簡化控制，同時為戰鬥部留下更大的彈內空間。在旋轉和迎角同時存在的情況下，彈體和尾翼上都產生馬格努斯力和力矩。彈體的馬格努斯效應機理與彈丸完全相同。
在翼身組合體中，尾翼的馬格努斯效應是由翼一體間干擾，斜置、斜切翼和尾翼鈍後緣底部壓強的變化引起的。實驗表明，翼一體間干擾與其他兩種原因相比較是次要的。
翼身組合體以正攻角旋轉前飛時，位於彈體背風面的上翼面將處於彈體的渦跡區內，該翼片將減小由於旋轉附加攻角而提供的當地升力，這樣上下翼片將合成一個側向力一馬格努斯力。由於彈體的馬格努斯力與尾翼上的馬格努斯力方向相反(如圖所示)，所以，在不同攻角下，渦跡對尾翼的影響產生的側向力大小不同，從而，全彈的馬格努斯力隨迎角變化將會或正、或零、或負，出現典型的非線性效應，這種由翼體干擾產生的馬格努斯力很難在理論上導出計算公式。
