庫塔-儒科夫斯基假定

庫塔-儒科夫斯基假定是空氣動力學中有關力學性質的假設，計算在機翼或是二維物體（例如圓柱）在均勻流體中的升力，且此流場的速度夠快，使物體的速度場是穩定及無分離的。假設是有關一個正圓柱的升力以及圓柱和流體之間的相對速度、流體密度以及環量。

基本介紹

• 中文名：庫塔-儒科夫斯基假定
• 外文名：Kutta - kutsky hypothesis
• 學科：力學
• 計算：二維物體在均勻流體中的升力
• 領域：空氣動力學
• 有關術語：環量

簡介

庫塔-儒科夫斯基假定得名自德國科學家馬丁·威廉·庫塔及俄國科學家尼古拉·葉戈羅維奇·茹科夫斯基，他們在二十世紀初首次提出這様的概念。庫塔-儒科夫斯基假定是考慮壓力及升力的無粘性理論，不過在典型的空氣動力學應力時，可以模擬實際的黏性流。

庫塔-儒科夫斯基假定建立升力和環量的關係，類似馬格努斯效應建立旋轉和側向力的關係一樣。不過此處的環量不是因為機翼的旋轉而產生，而是因為以下提及的機制而產生。由於機翼的存在，氣流的變化可以視為平移流場及旋轉流場（渦旋）的疊加。此旋轉流是由翼型的外傾角、攻角及銳利的後緣角所產生，不同於外形像龍捲風的渦旋。若離機翼夠遠時，旋轉流可以視為是由渦旋所引發的，渦旋的中心線平行二維平面。在描述機翼的庫塔-儒科夫斯基假定時，一般會假設機翼是圓柱形或是其他的茹科夫斯基翼型。

升力公式

此定理和在二維流場中的翼型（或是翼展無窮大的圓柱）有關，可以計算單位翼展下的升力。當環量 已知，其升力 除以翼展下的單位翼展升力（或表示為）可以表示為以下的方程式(1)：

其中：

及 分別為流體密度及在翼型上游，遠離翼型位置的流體速度，

為以下線積分定義的環量（逆時針為正值）

上述環量是沿著一個封閉圍道 進行，此圍道包覆著翼型或是圓柱，且沿著其正方向（逆時針）進行。其路徑需在位流的範圍內，不能在圓柱的邊界層內。被積分式是局部流體速度沿著曲線 切線方向的分量，且 為曲線 的無窮小面積。方程式(1)是庫塔-儒可夫斯基定理中的一個形式。

Kuethe和Schetzer用以下的話描述庫塔-儒可夫斯基定理：

任意截面積的柱形物體，其單位長度的受力等於，方向和垂直。

在使用庫塔-儒可夫斯基定理時，需注意環量的計算。

環量和庫塔條件

環量是流體的速度沿著一條閉曲線的路徑積分，通常用 來表示。如果 是流體的速度，是沿著閉曲線 的單位向量，那么：

環量的量綱(因次式)是長度的平方除以時間。

一個產生升力的翼型或者具有彎度，或者是在均勻的流體中以一定攻角（機翼弦線和平移方向的角度）平移。而且翼型需要有一個銳利的後緣。上述條件類似鳥的翅膀，有銳利的後緣，有彎度，在天空中有一定的攻角。

實際的流體是有黏性的，流體速度在翼型邊緣為零，因此若考慮黏性流體，且以翼型形狀為圍道計算環量，其環量也為零。甚至由翼形上方及下方的流體會在後緣相會，而黏滯耗散會使流體不旋轉。這稱為真實流場的庫塔條件。普朗特發現若雷諾數夠大，攻角夠小，翼型夠薄，則流場可以分為靠近機翼小區域的黏滯層（稱為邊界層），以及其他區域的非黏性流。

庫塔和儒可夫斯基發現計算雷諾數夠大，攻角夠小，厚度夠薄的翼型之壓力和升力時，若假定已考慮庫塔條件，可以假設整個流場是非黏性流。這稱為位流理論，在實務上結果相當接近。在非黏性流施加庫塔條件相當於計算環量。

簡單來說，類似鳥翅膀的機翼自然會產生升力，在飛行中的流場滿足庫塔條件。若使用位流理論（在計算壓力及升力時假設是非黏性流及無旋轉流，計算阻力時用普朗特邊界層來近似），要求飛行時間符合庫塔條件，會得到一個由=庫塔-儒可夫斯基定理和環量產生的升力，和實際的升力非常接近。

較複雜情形下的升力

庫塔-儒可夫斯基定理預測的升力是以無粘性流的勢流理論為基礎，但若流場是穩定且無分離的，庫塔-儒可夫斯基定理的結果很接近實際的黏性流。

在推導庫塔-儒可夫斯基定理時，有假設流場是無旋轉流，若在物體外有自由渦流，就像許多不穩定流的情形，此流場為旋轉流，在推導升力時就需要一些更複雜的理論。

小攻角下突然啟動的流場：若是機翼突然加速，或是攻角較小的情形下突然啟動的流場，在機翼後緣會連續的出現渦片泄離，此時的升力是時變不穩定的。若是小攻角下啟動的流場，渦片會延著平面的路徑，升力係數的曲線會隨時間而變化，其形式會是Wagner函式[7]。此時最終升力會如同庫塔-儒可夫斯基定理所預測的一樣，但初升力只有最終升力的一半[8]。當機翼前進七倍翼弦的距離時，其升力才會達到最終升力的90%。

大攻角下突然啟動的流場：若攻角夠大的話，機翼後緣的渦片一開始會是螺旋形的，理論升力在一開始會是無限大[9]。一般認為升力的曲線是隨時間單調遞增的，但在大攻角下，會有一段很短暫的時間會有升力下降的情形。

大攻角下啟動，有銳利的機翼前緣：若針對一片平粄，也有銳利的前緣，渦片泄離會出現前緣，而前緣的渦片泄離有二種不同的效果：

1.若仍接近前緣，可以提升Wagner升力曲線，可以增加升力。

2.若前緣的渦片泄離和後緣有關，引入新的後緣螺旋形渦片，延著升力增加的方向移動，則會破壞升力。

對於這種流場，渦升力線（VFL）可以用來了解不同情形下渦流帶來的效果（包括流場啟動及其他的條件），也可以控制渦流以增強或降低升力。渦升力線圖是一個二維的圖，其中會繪出渦升力線，其對升力的貢獻和其速度、環量及渦升力線和流線的餘弦成正比，因此渦升力線可以看出渦流對升力的提升或破壞程度。

Lagally定理：若在機翼外面有固定的渦源，其對升力的修正可以表示為渦源的強度，及因其他因素造成渦源處誘導速度，這稱為Lagally定理。

針對二相的非黏性流，傳統的庫塔-儒可夫斯基定理預測阻力為零，不過若機翼外有渦源，會產生阻力，其形成原因類似升力。

茹科夫斯基變換

茹科夫斯基變換（Joukowsky transform）是一種用於翼型設計的共形映射，以俄羅斯科學家尼古拉·茹科夫斯基的名字命名（不過最初是由德國數學家奧托·布盧門塔爾提出的）。該變換為：

這一變換將原空間中的復變數映射為新空間中的復變數。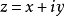

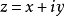
在空氣動力學中，茹科夫斯基變換可以用來求解繞茹科夫斯基翼型的二維勢流。所謂茹科夫斯基翼型，是指 平面中的圓經茹科夫斯基變換在z平面中得到的形狀。改變圓心坐標可以改變所得翼型的形狀。點 在圓的內部，而點則在圓上。

茹科夫斯基翼型的後緣處為一尖點。茹科夫斯基變換可以看成是卡門－特雷夫茨變換（Kármán-Trefftz transform）的特例。卡門－特雷夫茨翼型的後緣角是可變的，當後緣角為0時，即是茹科夫斯基翼型。