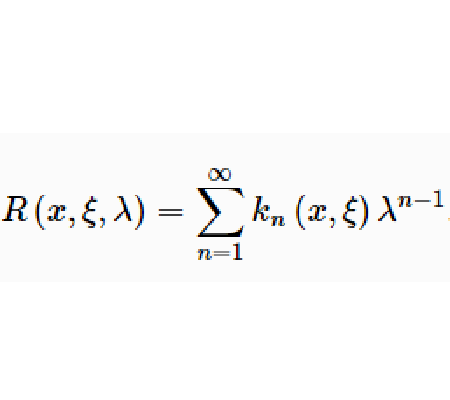預解核

預解核(resolvent kernel)是用來給出積分方程解的一種積分表示，利用它可以研究積分方程的有關性質。

基本介紹

• 中文名：預解核
• 外文名：resolvent kernel
• 所屬學科：數學
• 所屬問題：積分方程
• 相關概念：積分方程、半純函式等

基本介紹

預解核(resolvent kernel)是用來給出積分方程解的一種積分表示，利用它可以研究積分方程的有關性質。設 是積分方程

的連續核，則 由遞推公式

產生的 稱為 的n次疊核，它滿足公式

當

時，級數

在 上絕對且一致收斂，其和記為

此級數稱為諾伊曼級數， 稱為積分方程的預解核。預解核是λ全平面上的半純函式，它在任一有界域內只可能有有限個極點，每個特徵值就是預解核的極點。利用預解核，積分方程的解可表示為

這個結果在L²空間也同樣成立，即設 和 都是平方可積函式，且

記

和

則近似解序列

在 內絕對且一致收斂，其極限函式給出方程的惟一解。

預解方程

方程

稱為第二種弗雷德霍姆(Fredholm)方程，其中 是常數。

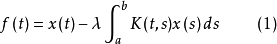
定理 (預解方程)弗雷德霍姆方程(1)的預解核滿足方程

及

式(2) 與(3)稱為方程(1)的預解方程。對給定的 如果存在滿足(2) 與(3)式的預解核 ，則稱 為核 的正則值。

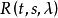
預解核的構造

設 為X 上的一個核。一個函式 稱為V-上屬(V-dominant)，如果對所有 若 在 上成立，必有 若常數1是 上屬，則稱V滿足完全的極大值原理。

命題1 若 為X 上的子Markov 預解核而V為 的位勢核，那么每一個 上中位函式是V上屬。特別，V滿足完全的極大值原理。

引理設 又設u為V上屬函式使得 且 那么 。

推論 對每個 線性運算元 是一個單映。若 且 則 。

命題對每個 是一個代數同構。

命題對每個 線性映射 是正的且 對所有

命題 是X上的一個子Markov 預解核且V為 的位勢核。

定理 設V為X上的有界核。那么X 上存在一個子Markov 預解核使得的充要條件是V滿足完全的極大值原理。這預解核是由V唯一確定的。

定理設且則下述結論成立：

1. 存在唯一的子Markov 預解核使得且是關於P的位勢核。

2. 對每個嚴格的。.

3. 是嚴格的。

命題設用F表示這樣的全體構成的集：與存在使得那么F是增加的濾子且。

命題設為關於p的位勢核。那末，對每個，下面命題等價：

(1)

(2) 存在使得且。

推論設且使得又設V為關於p的位勢核。那么，對每個存在中的序列使得增加收斂於且對每個為A 的緊子集。