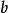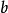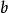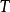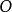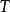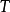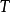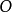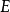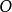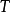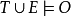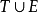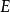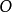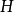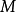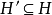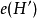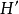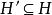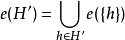非演繹推理

推理是利用顯式儲存的知識以產生另外顯式知識的過程。推理過程也可分為兩類，即演繹推理與非演繹推理。演繹推理，就是從一般性的前提出發，通過推導即演繹，得出具體陳述或個別結論的過程。非演繹推理是指結構化表示下的繼承性推理，也是一種基本推理，數學證明中已存在但尚未認知的基本定理。由於知識處理的需要，提出了多種非演繹的推理方法，如連線機制推理、類比推理、基於示例的推理、反繹推理和受限推理等。

基本介紹

• 中文名：非演繹推理
• 外文名：非演繹推理non-deductive inference
• 學科：邏輯學
• 定義：數學證明已存在尚未認知基本定理
• 有關術語：演繹推理
• 套用：人工智慧

定義

演繹推理是數學工作者經常要用的一種數學思維形式，演繹推理的作用在於從已知的知識得到未知的知識。非演繹推理是是已經存在但尚未認知的推理，非演繹推理的作用同樣在於從已知的知識得到未知的知識。它的使用方法大致可分為三種:一是作為定理的全部證明，關於這一點下面還要提到；一是作為演繹推理的前提分析，這是最常見的一種；一是作為演繹推理的結論分析。非演繹推理是對薄萊爾預備定理證明中的演繹推理的結論進行分析。非演繹推理的使用方法，需要對反證法作點說明。

演繹推理與非演繹推理有共同之處也有不同之處。共同之處在於：第一，二者都是從前提推出結論；第二，非演繹推理除歸納法之外，與演繹推理一樣，只要前提都真，則結論必真；第三，二者的作用相同，都是從已知的知識得到未知的知識；第四，二者都有一個前提分析過程。不同之處在於:第一，演繹推理從前提到結論之間的推理用的是邏輯推理；而非演繹推理的推理是根據具體問題具體分析進行的。由於非演繹推理與定理條件及證明方法等具體情況密切結合，因此在非演繹推理之中常常顯示出推理的艱難、推理的技巧及推理的水平；第二，演繹推理的推理不涉及命題本身的內容，而非演繹推理的推理則不然；第三，演繹推理的前提與結論之間的關係必然為數理邏輯的邏輯演算中的形式定理所反映，而非演繹推理的相應關係則不能；第四，演繹推理對應著一個演繹推理規則，而非演繹推理則沒有。

類比推理

類比推理是人類核心的認知能力之一，關注個體的認知發展，離不開對類比推理的探討。類比推理簡稱類比，它是人類抽象邏輯的重要形式。從形式邏輯的角度講，類比推理是指從兩個（類）對象的相似性和一個（類）對象的已知特徵推出另一個（類）對象也具有這個特徵的過程。 研究中一般都採用上述定義，但要充分理解類比推理的內涵，與其實驗任務是密不可分的。類比推理是哲學、邏輯學和心理學等學科研究的重要內容，是人類能夠進行整合思維活動的重要機制，也是保證個體有效學習的工具。它的產生、發展和成熟是個體認知活動順利完成的主要保障。類比推理的研究始終沿著兩條路線前進:一條是研究類比推理的本質，另一條是研究類比推理與問題解決關係。儘管這些方面的研究獲得了被學者們認同的結論，但在源類比物性質、過程限制及知覺特徵對目標類比物的影響上，則存在不同主張。有代表性的理論如下：

結構映射理論(structure mapping theory)該理論是由Gentner.D(1983)提出來的，其基本思想是，類比中最關鍵因素是源類比物與目標類比物之間的聯繫。要實現這種聯繫，必須具備三個特徵：一是結構連續性，即形成平行結構和一對一的對應關係。前者需要關係和主題的共同匹配，後者要求表征內的每個要素都要與另一表征內的要素形成匹配。二是以關係為中心性，即它要求類比物必須包括共同的關係而不是共同特徵。三是系統性，即趨向於形成關係體系的匹配。例如，當一種結構上的聯繫給定後，就會從類比中產生進一步的推理，其含義是，系統性所蘊涵的意義在於產生自發性的推理。由此說來，結構映射理論對類比推理中關係的性質、特徵要求很高，即對類比物的一致性、公平性和可匹配性要求更高。

多重限制理論，此理論的倡導者們(Keith Holyoak& Paul Thagard，1997)指出，類比的最後形成是由於在類比思維過程中大量結合在一起的總的限制所引起的：一是相似性限制，即類比在某種程度上是由於所含要素的直接相似所引起的；二是結構性限制，這種限制揭示的是類比映射和推理背後的關鍵的結構限制，就是在源類比物與目標類比物的各要素之間建立起連續的、一一對應的對應物的氛圍；三是目標限制，要求推理者的目標與類比的目的(要解決什麼問題)建立聯繫。從可被限制類比推理過程的因素來看，限制物越多，類比推理進行越困難。

高水平知覺理論，該理論(B.Markman，1997)指出，人的知覺分低、高兩種水平。前者包括各種感覺中的信息加工過程；後者包括對低水平知覺加工的信息進行總體把握，並從這些精確的材料中提取意義，使之在概念水平上對情境進行知覺。這個範圍包括從對事物的再認到抓住事物間抽象的聯繫，到對整個情境的理解和把握。即類比包括情境知覺過程和映射過程。在前個過程中，負責對材料過濾和組織，形成情境的心理表征。在後個過程中，同時激活兩個情境表征，並形成一對一的對應，進而產生最後的類比。這兩個過程是相互作用、不可分割的，即每個映射過程都需要知覺過程產生表征，而每一個知覺過程都需要映射過程的參與才能成為有意義的知覺。情境知覺水平越高，情境表征就越清晰，類比推理效果就越好。

反繹推理

溯因法或溯因推理（abductive reasoning，也譯作反繹推理），是推理到最佳解釋的過程。換句話說，它是開始於事實的集合，並推導出其最佳解釋的推理過程。有時使用術語溯因（abduction）意味生成假設來解釋觀察或結論，但是前者定義在哲學和計算二者中更常見。

演繹：允許推導 作為 的結論，換句話說，演繹是推導已知事物的推論；

溯因：允許推導 作為 的解釋，溯因同演繹反向，通過允許“ 蘊涵 ”的前件 推導自結論 ；換句話說，溯因是解釋已知事物的過程。在邏輯中，溯因法通過表示領域的邏輯理論 和觀察的集合 進行的。溯因是依據 推導 的解釋的集合。 要成為 依據 的解釋，它應當滿足兩個條件：

推導自 和 ；

相容於 。

在形式邏輯中，假定 和 為文字的集合。 是 依據理論 的解釋的兩個條件則形式化為：

；

是相容的。

在滿足這兩個條件的可能的解釋 之中，通常施加一些其他的最小性條件來避免無關的事實（對 的蘊涵沒有貢獻）包含在解釋中。

溯因法的一種不同的形式化是基於逆轉計算假設的可見效果的函式。形式化的說，我們給出假設的集合 和表現（manifestation）的集合 ；它們相關於領域知識，並以函式 所表示，這個函式接受假設的集合作為參數並給出對應的表現的集合作為結果。換句話說，對於假設的所有子集 ，它們的效果通過 來知道。

溯因法通過找到一個集合 ，使得 進行的。換句話說，溯因是通過找到假設的集合 ，使得它們的效果 包含所有的觀察 來進行的。

公共的假定是假設的效果是獨立的，就是說，對於所有的 ， 成立。如果這些條件滿足，溯因法就可看作集合覆蓋的一種形式。

連線機制推理

連線機制推理，更具體地說，就是以人工神經網路作為原型的知識表示方法。在人工智慧研究中，這種知識表示方法可以說歷經磨難。它的出現早於許多其它知識表示方法將近二十年，但在60年代末，由於尋找其有效學習算法的失敗及對其泛化能力的懷疑，導致這種知識表示方法退出了人工智慧的研究舞台，直到80年代初，人工智慧研究者才將這類知識表示方法的原理以連線機制這個術語重新納入人工智慧研究的範圍。當然使其在智慧型研究中占有一席之地的直接原因乃是 BP 算法的出現。儘管BP算法的成功是使其引起人工智慧研究重新注意的原因，但這不是全部，更重要的是這種知識表示方法可以刻畫那些使用局部表示難以描述的與感知類似的知識。例如，對於某些評價問題，領域的專家可以對他們熟悉的領域中的實例進行正確的評價，但是這些專家卻難以解釋對某個實例作出評價的理由，無論是統計意義下的理由，還是機理上的理由，而在多因素情況下甚至難以對這些因素進行排序，這就導致了使用局部表示的困難，即，大量的例外使系統難以承受，這就是知識的組合爆炸問題。從最佳化的角度來看，如果將實例理解為超平面上的一些點，原則上可以使用逼近理論來解決這個困難，但問題是什麼樣的數學基函式既可以給出在智慧型意義下的科學解釋而又存在方便的數學處理方法呢。BP算法的貢獻就是找到了符合這兩個條件的數學基函式，而這個數學基函式就是連線機制的知識表示方法。對這類知識表示方法除了上述的優點之外， 並行性也是其重要的特性。但是，這種知識表示方法也同樣存在顯著的缺點，主要是學習收斂速度及泛化能力問題。前者無需多說，而後者則是由於這種表示所定義的數學空間與自然界中的問題空間之間存在巨大差異所造成的，而且這個差異將隨問題規模的增加呈指數規律上升，其泛化能力則呈指數規律下降。從理論上還未找到有效的解決方法，而在技術上則採用與其它局部表示集成的方法來克服這個困難。基因表示與連線機制表示構成了知識表示體系樹中的另一分支。

歸納推理

歸納推理，又稱基於示例的推理，是一種由個別到一般的推理。由一定程度的關於個別事物的觀點過渡到範圍較大的觀點，由特殊具體的事例推導出一般原理、原則的解釋方法。自然界和社會中的一般，都存在於個別、特殊之中，並通過個別而存在。一般都存在於具體的對象和現象之中，因此，只有通過認識個別，才能認識一般。人們在解釋一個較大事物時，從個別、特殊的事物總結、概括出各種各樣的帶有一般性的原理或原則，然後才可能從這些原理、原則出發，再得出關於個別事物的結論。這種認識秩序貫穿於人們的解釋活動中，不斷從個別上升到一般，即從對個別事物的認識上升到對事物的一般規律性的認識。例如，根據各個地區、各個歷史時期生產力不發展所導致的社會生活面貌落後，可以得出結論說，生產力發展是社會進步的動力，這正是從對於個別事物的研究得出一般性結論的推理過程，即歸納推理。顯然，歸納推理是從認識研究個別事物到總結、概括一般性規律的推斷過程。在進行歸納和概括的時候，解釋者不單純運用歸納推理，同時也運用演繹法。在人們的解釋思維中，歸納和演繹是互相聯繫、互相補充、不可分割的。