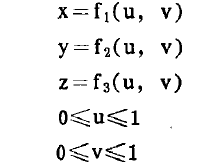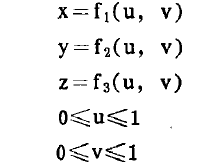當用線框模型來表示物體時，要消除不可見的線，即隱藏線的消除。
給出一個三維物體，要畫出確定的立體感強的投影視圖，必須決定形體上哪些線是不可見的，不可見的部分不顯示，這就是隱藏線消除問題。
基本介紹
- 中文名：隱藏線消除
- 外文名：Hidden line elimination
- 類別：計算機科學
- 基本步驟：數據準備、數據整理等
- 算法：多面體型算法等
- 領域：計算機圖示
概況,基本步驟,運算及操作,分類及檢索,最大最小方框判別,包圍檢驗,算法,多面體型算法,曲面體型算法,複合體型算法,
概況
隱藏線及隱藏面消除問題自六十年代中期以來一直是計算機圖示領域中一個十分活躍的分支。問題的提出在於隨著計算機圖示的套用日益廣泛，實用上對圖象的逼真性及立體感要求愈來愈高。早期所用的顯示設備限於劃線式顯示器，隱藏線消除技術成為競相研究的重點。後來光柵掃描顯示器日益普及，注意力又轉向隱藏面消除技術的研究。由於光柵掃描顯示設備解析度的限制及離散效應的影響，不能顯示圖象精細細節,加之掃描轉換速度不適應對話式顯示的要求，所以在高質量工程圖及對話式顯示方面線型圖具有獨特的優點,仍需深人研究。
基本步驟
隱藏線消除的基本步驟：
1.數據準備
為適應消去隱藏線的操作，連續的三維物體首先需要平面化。多面體自然由平面構成，曲而體可用一定數量的小平面來近似表示。這些平面及小平面統一用多邊形來表示(一般以四邊形為方便、多邊形可分解為四邊形)。經過這樣簡化，三維物體的幾何信息一般只需儲存各四邊形頂點的座標值以及頂點的連線關係。
座標信息按照套用場合進一步施以透視變換或平行投影變換。
2.數據整理
將數據進行分組與排序，以便於檢索及避免一些不必要的運算或操作。
3.初步判別
凡用簡捷方法就能判明可見性的部分不要放在下一步去做，如消去背影面往往可去除一半左右的基本元素，大大減少下一步判別的工作量。
4.比較判別
判定基本元素如格子點或格子線(四邊形的頂點及邊)是否可見或哪一部分可見。
5.連線成圖
按一定邏輯將可見點或線段連結起來。
運算及操作
分類及檢索
消除隱藏線的算法往往要處理大量數據，而且算法執行的各種操作又常在某些特定數據上進行。因而用恰當的方法(具體方法可參看有關專著)將數據按某種特徵分類排序，並採用快捷的檢素方法檢出所需處理的數據，這是提高整個算法的頻率的關鍵措施之一。
最大最小方框判別
對投影平面xy面上的一線段或一多邊形，通過其中具有xmax及xmin值的頂點(端點)且平行於Y軸的兩直線段與通過具有ymax及ymin。值的頂點(端點)且平行於X軸的兩線段圍成的矩形稱為最大最小方框。
若兩方框不相交，則可粗略地認為對應框內之多邊形或線段相互間不影響可見性。實現這種判別操作僅需簡捷幾步，適合於初步判別階段快速剔除大量可見性無關之元素，或在判別階段中用以迅速挑選比較對象。
包圍檢驗
判別一點是否被一多邊形包圍或被一多面體包圍是可見性判別時常用的操作。
利用平面方程可以判別一個點是否被多面體包圍。將該點座標值代入平面方程(一般式)，若方程右端不等於零，則表示該點位於平面一側。適當選擇方程係數的符號，可以判定一個點在多，面體內部還是在外部，若是前者則被包圍。
算法
隱藏線消除問題的算法儘管繁多，但每一算法都是為解決某一特定類型的問題而設計的。按照所處理的對象的幾何特性，現有算法可分類如下：
1.多面體型 2.曲面體型 3.複合體型
多面體型算法
這類算法處理由多面體構成的圖象。現有文獻中屬於此類問題者占有較大比重。最早提出多面體型隱藏線消除算法系L. G. Roberts，而Griffiths的算法是其中較簡易、不受圖象複雜程度限制而且可得到精細畫面的一個。
Griffiths的算法把多面體的棱邊作為基本元素，將其與多面體的每個面相比較，以判別棱邊上哪些部分被遮住而看不見，即所謂“邊一一面’比較法。
他採用右手坐標系。Y軸正向朝上，X軸正向指向觀察者右側。連結兩點(x1, y1, z1)與(x2,y2,z2)的直線段用下列方程表示
x=x1+
(x2-x1)
y=y1+(y2-y1)
z=z1+(z2-z1)
0
1
一條被檢驗的棱邊與視點(投影中心)構成一三角形，這個三角形與多面體中一個面(通常以多邊形表示)相交，其交線稱之為屏障線。利用屏障線可判定一棱邊的可見性。圖1所示中屏障線GN能影響被檢邊AF哪一段HM稱為有效段。求解AF與E形多邊形各邊的聯立方程可得屏障線與該多邊形的交點，因為HM與AF在X一Y面具有相同的透視投影。屏障線GN被分割成數段HI,IJ等，其分點亦用α來標識。利用各交點與多邊形頂點之關係可求出屏障線上各分點處的深度值，即Z坐標值。記被檢邊中點處深度值為Ze，屏障線中點處為Zm，若Zm
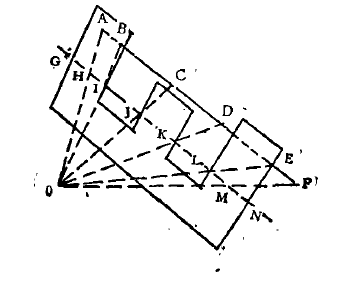
圖1
該算法在進行上述‘邊—面’比較前，先將X一Y面上為圖象所復蓋的面積劃分為縱橫排列的小方格，象方格紙一樣。這些小方格賦以標號，即用二維數組Cij來標識。圖象中表示多面體各面的多邊形按其所落入的方格序號迸行編組，並按多邊形頂點中之最小深度值為關鍵值，將每組內的多邊形遞降排序。被檢驗的一邊可能跨過若干小方格，在進行‘邊—面’比較時，僅需將此邊與其跨過的小方格中之多邊形比較，因為其它面不會影響該邊的可見性。侯所有邊經逐一比較判別，算法即告結束。
多面體算法的特點是以邊為基本判別元素。因多面體各表面用多邊形表示，而多邊形又山各邊確定。邊的可見性確定之後，整個圖象之可見情況將隨之一目了然。不同算法之區別在於它們採用不同的數據結構，不同的比較判別方法，如用‘邊—邊’比較，‘邊—多面體’比較等。
曲面體型算法
這類算法處理的對象是由複雜曲面(自由曲面或雕塑曲面)組成的。迄今公開發表的算法不多，據Ohno統計僅有三個。
曲面體通常由若干曲面塊組成，曲面塊間是光滑連續的。一曲面塊以參數方程表示：
這類算法以格子點作為基本元素，逐一檢驗其是否可見。現有三個算法採用相同的判別準則，是由Appel首先提出的。曲面上一格子點是否可見，可通過逐一檢驗圖中的四邊形，看其是否遮住這個點，稱之為‘點—面’比較法。
一個點若同時滿足以下兩個條件即認為是不可見的：
①點相對於與之比較的四邊形，位於視點之異側。
②點之投影落人該四邊形投影面積之內。
Ohno的算法最為簡明，處理速度最快。該算法在進行‘點—面’比較前作如下準備：
1)將剛剛包容著一曲面塊的平行六面體空間分割為較小的子空間(亦為平行六面體)，每一子空間所含的該曲面塊上的四邊形編為一組，每組中又按四邊形頂點中之ymax遞降排序。
2)曲面塊上格子點Rij進行透視變換。一四邊形經透視變換後的形狀石作巷仍為四邊形，或成為三角形，或呈直線段等，總共歸納為51個類型，編成一個型譜。
進行‘點—面’比較時，沒有必要將全部四邊形對一點比較，只與包含該格子點或位於該格子點與視點間的子空間內的四邊形相比較，就足以判定該格子點是否可見。
上述準備工作有利於加速比較判別過程，這是Ohno算法的特點。
當全部格子點經比較，判明是否可見，然後分別對點陣進行行及列掃描。設A, B為被掃描的相鄰點。
若A, B均可見，則連結A, B；
若A, B均不可見，掃描下一點；
若A, B中僅有一點可見，則按對分法選新檢驗點，調用同一‘點—面’比較過程，直到找出AB間可見與不可見的分界點，連可貝點與分界點。
Griffiths的算法與Ohno的區別是當全部格子點直接經‘點—面’比較判明可見性後，將圖中可見部分與不可見部分的分界線粗略地連線起來。這條分界線是通過有關格子線(其兩端點中，有一是可見的，另一是不可見的)中點的多邊形。然後用基於解非線性方程組的數值方法求解分界點的精確位置，從而確定分界線的準確形狀。這條分界線實際上就是輪廓線。將輪廓線所包圍的區域復以細密的格子線然後轉換成最終的線型圖。
曲面體算法主要進行兩種操作，一是通過‘點—面’比較判明格子點的可見性，其次是確定相鄰格子點間可見部分與不可見部分的分界點(如果存在的話)。將相鄰之可見點連結起來就是最後的答案。
複合體型算法
這類算法處理由多面體及曲面體複合構成的圖象，也可以說是上述兩種模型之綜合。此類模型在工程中最為常見。
由前可知，多面體投影圖中，以邊為基本元素，相關邊圍成的多邊形代表多面體的面;曲面體圖中則以格子點為基本元素，相關格子點構成的四邊形作為曲面體表面上的局部線性近似(曲面體的線型圖實際上是曲面體的一種近似表示)。在本作者的算法中將上述多邊形的邊及四邊形的邊均定義為複合體模型的邊，並以邊為基本元素，與相關的四邊形(為處理方便，多邊形可分解為四邊形)逐一比較以判明其可見性。判別一邊的可見性按如下準則：
1)一條邊完全可見，若滿足下列條件之一
a)兩端點位於四邊形平面之前(近觀察者)；
b)兩端點投影落在四邊形投影面積之外，且該邊與四邊形投影不相交，
c)其中一端點之投影落人四邊形投影面積之內，但位於四邊形平面之前。
2)一條邊完全不可見，若其兩端點投影落入四邊形投影面積之內，且位於該四邊形平面之後(遠離觀察者)。
3)其餘情況屬部分可見。
以上準則假定非相鄰表面不互相貫穿。這種判別方法屬於‘邊—面’比較法。
本算法的預處理，首先是去除全部背影面，其次是利用隨機方框來選擇比較對象。所謂隨機方框就是一個矩形，它以被檢驗的邊為對角線，兩對邊分別平行於投影面基本坐標軸。顯而易見，只有那些落入該框內的四邊形才有可能影響被檢邊的可見性。
這個算法的特點是不僅可處理複合體模型而且亦可處理多面體及曲面體模型，既可輸出格子線式富立體感的圖象也可輸出輸廓圖。因而是一個通用算法。
