隨機網路,也稱計畫評審技術(PERT)，是一種反映多種隨機因素的網路技術。與傳統的網路技術不同，隨機網路技術模型中的節點、箭線和流量均帶有一定程度上的不確定性，不僅反映活動的各種定量參數，如時間、費用、資源消耗、效益、虧損等是隨機變數，而且組成網路圖的各項活動也可以是隨機的，按一定的機率發生或不發生，並且允許多個原節點或自多個匯節點的網路循環迴路存在。
基本介紹
- 中文名：隨機網路
- 外文名：PERT
- 又名：計畫評審技術
- 定義：反映多種隨機因素的網路技術
- 學科：信息科學
發展,特點,構成,解題步驟,
發展
60年代，美國國防部在阿波羅空間系統研究、製造和發射過程中，首次建立了隨機網路模型，並提出了分析和求解隨機網路的方法，用以確定該系統的最終發射時間，協調各承包商的工作進度，取得了明顯的效果。
特點
與普通網路圖比較，隨機網路具有以下幾個特點：
- 隨機網路的箭線和節點不一定都能實現，實現的可能性取決於節點的類型和箭線的機率係數；
- 隨機網路中各項活動的時間可以是常數，也可以是服從某種機率分布的密度函式，更具有不確定性；
- 隨機網路中可以有循環迴路，表示節點或活動可以重複出現；
- 隨機網路中的兩個中間節點之間可以有一條以上箭線；
- 隨機網路中可以有多個目標，每個目標反映一個具體的結果，即可以有多個起點或終點。
構成
一、節點符號表示方法：
1、輸入部分，如圖1所示
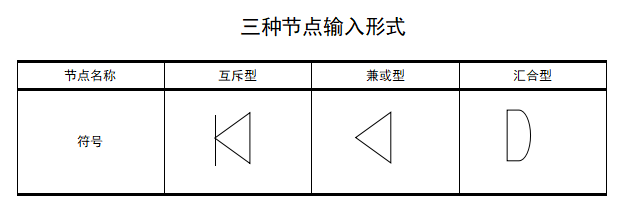圖1
圖1第一種形式：互斥型
第二種形式：兼或型
第三種形式：匯合型
2、輸出部分，如圖2所示
第一種類型：肯定型
圖2
圖2第二種類型：隨機型
對於一張隨機網路圖既有起止節點，又有中間節點。由於中間節點有輸入部分，又有輸出部分，節點需同時能表達不同的輸入關係和輸出類型，上述不同節點的輸入和輸出形式可以組合成六種節點形式。如圖3。
二、箭線及傳遞係數的表示方法
圖3
圖3隨機網路的箭線可以表示具體的活動，也可以表明一項活動的結果，或者兩項活動之間的關係。為了表達活動的時間、成本、效率，還必須進一步說明實現各項活動的有關參數，即節點之間通過箭線傳遞的係數。
常用的傳遞係數有兩類：時間或費用係數，反映活動所需的消耗；機率係數，反映活動實現的可能性及質量合格率等。
解題步驟
隨機網路的解題步驟可歸納為以下幾點：
1、針對所研究的系統和問題，反覆考慮和剖析，找出能反映計畫模型的主要因素，按照活動的邏輯關係，選擇合適的節點類型，繪製出隨機網路計畫模型。
2、收集有關網路圖中傳遞係數的必要資料，並儘量使其符合實際，保證模型係數的準確性。若活動時間不能用常數表示，可以估一個均值和方差，或者確定一個大致範圍，再選擇一個合適的機率分布密度函式，做到有據可依。
4、通過計算，求出隨機網路最終所需時間及實現機率。根據矩母函式，在S=0時，其值為1，即，求得特定節點的實現機率；在求得節點實現的條件機率後，根據，求得特定節點實現的期望值。另外，根據需要，還可以求出所需成本等其他必要的參數。
5、根據計算結果，進一步分析該網路系統，對不同方案或不同問題進行綜合評價，並進行必要的調整和修改。
