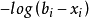障礙函式(barrier function)亦稱內懲罰函式、圍牆函式或碰壁函式，是一類制約函式。
在數學領域約束最佳化中，障礙函式是一個連續函式，其中點的值隨著點到達最佳化問題的可行區域的邊界而增加到無窮大。這些函式用於通過更容易處理的目標函式中的懲罰項來代替不等式約束。
兩種最常見的屏障功能類型是反向屏障功能和對數屏障功能。 恢複對數屏障功能是由於它們與原始雙重內點方法的聯繫。
基本介紹
- 中文名：障礙函式
- 外文名：Barrier function
- 學科：數學
- 別稱：圍牆函式、碰壁函式
- 作用：處理函式懲罰項代替不等式約束
- 相關名詞：目標函式
介紹,障礙函式法,原理,算法過程,罰函式法,基本思想,分類,優缺點對比,對數屏障功能,更高的維度,正式定義,與障礙函式法,
介紹
障礙函式(barrier function)亦稱內懲罰函式、圍牆函式或碰壁函式，是一類制約函式。
在數學領域約束最佳化中，障礙函式是一個連續函式，其中點的值隨著點到達最佳化問題的可行區域的邊界而增加到無窮大。這些函式用於通過更容易處理的目標函式中的懲罰項來代替不等式約束。
兩種最常見的屏障功能類型是反向屏障功能和對數屏障功能。 恢複對數屏障功能的興趣是由於它們與原始雙重內點方法的聯繫。
障礙函式法
（內點法）
原理
設有純不等式約束問題minf(X)：s.t.gi(X)≤0,i=1,2,…,m，設原問題內部非空，初始點X0選為內點。障礙函式法（內點法）構造的增廣目標函式形為F(X,γ)=f(X)+γB(X)，其中，γ>0,B(X)>0（當X為內點），且當X在邊界時，B(X)的值為無窮大。這樣，可阻止F(X,γ)的極小點穿越邊界，而必定被限制為可行點。
下面再討論障礙因子γ的結構。先看一個簡單的例子，設原問題為：
minf(X)
s.t.–x+1≤0
其增廣目標函式為
F(x,γ)=f(x)+γB(x)=x+γ(x–1)
原問題的精確極小正好是x=1。
在一般條件下，可以證明，F(X,γ)的無約束極小點Xγ恆為可行域的內點，且當γ→0時，Xγ趨於原問題的約束極小點。
障礙函式法（內點法）
算法過程
（1）取X0為內點，γ0>0（通常，取γ0=0），障礙因子縮小係數d,0<d<1，k=0,ε>0；
（2）構造增廣目標函式F(X,γk)=f(X)+γkB(X)
（3）以Xk為初始點，求解無約束最佳化問題minF(X,γk)
設其無約束極小點為Xk+1；
（4）如果0<γkB(Xk+1)≤ε，輸出Xk+1，計算停止；
否則，γk+1=dγk，k=k+1轉（2）。
註：從理論上講，Xk一定是可行域的內點，但是在實際計算過程中，由於步長是取離散數值，以及捨入誤差等原因，使Xk有可能取為非可行點，在這種情況下，應選用優於Xk+1的內點來取代Xk。
罰函式法
（外點法）
罰函式是指在求解最最佳化問題(無線性約束最佳化及非線性約束最佳化)時，在原有目標函式中加上一個障礙函式，而得到一個增廣目標函式，罰函式的功能是對非可行點或企圖穿越邊界而逃離可行域的點賦予一個極大的值，即將有約束最最佳化問題轉化為求解無約束最最佳化問題。
基本思想
把非線性約束最佳化問題轉化為無線性最佳化約束問題。依據如何將目標函式和約束函式進行組合，人們導出了許多不同形式的罰函式。由於這些早期方法均需要求解一系列無約束的罰函式極小化問題，故通常稱之為序列無約束極小化方法(Sequential Unconstrained Minimization Technique)，簡稱SUMT。
基本思路：通過引進一個乘法因子把約束條件連線到目標函式上，從而將有約束的最最佳化問題轉化為無約束條件的問題。合理的罰函式可以在當搜尋到不可行點時，是目標函式值變得很大，離約束條件越遠懲罰越大。
分類
（1）外罰函式法
根據約束的特點，構造某種懲罰函式，然後加到目標函式中去，將約束問題求解轉化為一系列的無約束問題。這種“懲罰策略”，對於無約束問題求解過程中的那些企圖違反約束條件的目標點給予懲罰。
通過上述方法，我們可以把有約束的問題化為無約束問題求解。也就是所謂的外罰函式法。
但是外罰函式的原理主要是套用了近似最優並且近似可行的，近似最優可以接受，但是近似可行在實際運用中讓人無法接受。這一點可以由內罰函式解決。
（2）內罰函式法
相比於外罰函式法在不可行區域加懲罰，內罰函式法在可行域邊界築起高牆，讓目標函式無法穿過，就把目標函式擋在可行域內了。
但是這種懲罰策略只適用於不等式約束問題，並要求可行域的內點集非空，否則，每個可行點都是邊界點，都加上無窮大懲罰，懲罰也就失去意義了。
優缺點對比
2）內點法適用於解含不等式約束問題，並且每次疊代的點都是可行點，這是設計人員所希望的。但要求初始點為可行域的內點，需要相當的工作量，同時它不能處理等式約束；外點法適於解既含等式約束又含不等式約束的最佳化問題，初始點可以是可行域之外的點，卻不能保證近似最優解是可行的。
3）罰函式法對於增廣的目標函式的Hessian矩陣的條件數隨罰因子增大或減小而增大，造成在求解無約束最最佳化問題時的困難，如何選擇罰因子往往進退維谷。如外罰函式法，欲使得無約束問題接近於原約束問題，應該選擇儘可能大的罰因子；但為了減輕求解無約束問題的困難，又應選取較小的罰因子，否則增廣矩陣病態。這也是罰函式法的固有弱點。
對數屏障功能
對於對數屏障功能，當x <b時，g（x，b）被定義為-log（b-x）（在1維中，更高維度中的定義見下文）。 這基本上依賴於log（t）趨向於負無窮大的事實，因為t趨向於0。
這引入了一個梯度給最佳化的函式，它有利於x（在這種情況下值低於b））的極限值，同時對遠離這些極端的函式的影響相對較小。
取決於所最佳化的功能，對數屏障功能可能比較少計算昂貴的反屏障功能有利。
更高的維度
擴展到更高的維度是很簡單的，只要每個維度是獨立的。 對於應限制為嚴格低於bi的每個變數xi，添加
正式定義
在
上最小化CTx
假設下式可行：
定義對數屏障
與障礙函式法
罰函式法與障礙函式法是求解約束極小化問題的較好的算法，其基本原理是在原目標函式中加上一個罰（障礙）函式，而得到一個增廣目標函式。罰（障礙）函式的功能是對非可行或企圖穿越邊界而逃離可行域的點賦予一個極大的函式值。可以作一個形象的比喻：在約束極小化問題中，約束條件是一條“法律”，凡是不服從這條“法律”的點被處以“罰款”的“經濟制裁”，而且“罰款”的數額極高。這樣，在對新的目標函式進行無約束極小化的過程中，就會迫使疊代點逐步逼近（當疊代點在可行域外時）或者不能離開可行域（當疊代點在可行域內時），這樣所得的關於增廣目標函式的無約束極小化的解就會逼近於原目標函式的約束極小化的解。也就是說，可以將約束極小化問題通過增廣目標函式而化成無約束極小化問題，而後者可以用前幾節所介紹的算法來求解。
