阿達馬不等式(Hadamard inequality)是一種特殊不等式,指矩陣的子行列式所滿足的一個不等式。設V是n維歐氏空間,V中向量α1,α2,…,αs的格拉姆矩陣A的行列式的平方小於等於諸向量αi的內積的乘積,由此可導出阿達馬不等式。
基本介紹
- 中文名:阿達馬不等式
- 外文名:Hadamard inequality
- 所屬學科:數學
- 所屬問題:高等代數(矩陣)
- 簡介:矩陣的子行列式滿足的不等式
基本介紹









相關介紹
































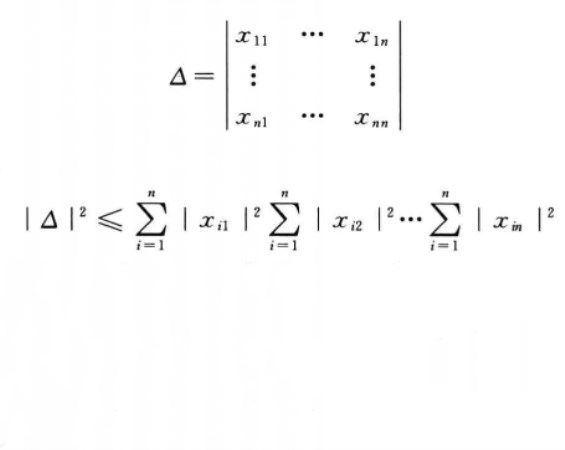
阿達馬不等式(Hadamard inequality)是一種特殊不等式,指矩陣的子行列式所滿足的一個不等式。設V是n維歐氏空間,V中向量α1,α2,…,αs的格拉姆矩陣A的行列式的平方小於等於諸向量αi的內積的乘積,由此可導出阿達馬不等式。









































阿達馬不等式(Hadamard inequality)是一種特殊不等式,指矩陣的子行列式所滿足的一個不等式。設V是n維歐氏空間,V中向量α1,α2,…,αs的格拉姆矩陣A的行列式的平方小於等於諸向量αi的內積的乘積,由此...
他為偏微分方程創造了適定問題概念。他也給了其名字——論體積的阿達馬不等式,還有阿達馬矩陣,是阿達馬變換所以建立的。量子計算的阿達馬門使用這個矩陣。在阿達馬所著的《數學領域的發明心理學》(Psychology of Invention in the Mathematical Field),他用內省來描述數學思維過程。與把認知和語言等同的作者截然相反...
則存在阿達馬不等式:若且唯若M是阿達馬矩陣式上式取等號。阿達馬矩陣的階數必須是1,2,或者是4的倍數。西爾維斯特構造法 阿達馬矩陣最初的構造的例子是由[[詹姆斯·約瑟夫·西爾維斯特]]給出的。假設''H''是一個''n''階的阿達馬矩陣,則下面的矩陣 給出一個2n階的阿達馬矩陣。連續使用這個方法,我們可以...
等式(1)和不等式(2)給出下面的定理:定理3 對於存在秩為4m的(規範)阿達馬矩陣的所有m,有:這個界是通過使用(4m-1)阿達馬碼得到的。設B(n,d)是長度為n的字的最大數量,其中每一個字與其他字之間的距離都正好是d,顯然,B(n,d)≤A(n, d)。推論4對於存在秩為4m的規範阿達馬矩陣的所有m,有 證...
1.5.2 行列式的阿達馬不等式 30 1.5.3 正則變換的廣義處理 31 1.5.4 無窮多個變數的變線型和二次型 34 1.5.5 無窮小線性變換 35 1.5.6 微擾 36 1.5.7 約束 38 1.5.8 矩陣或變結型的初等除數 38 1.5.9 復正交矩陣的譜 39 參考文獻 39 第2章 任意函式的級數展開 41 2.1 正交函式組...
